Предмет: Алгебра,
автор: Fhvgjjcswhoknb
Помогите решить систему уравнений
Приложения:
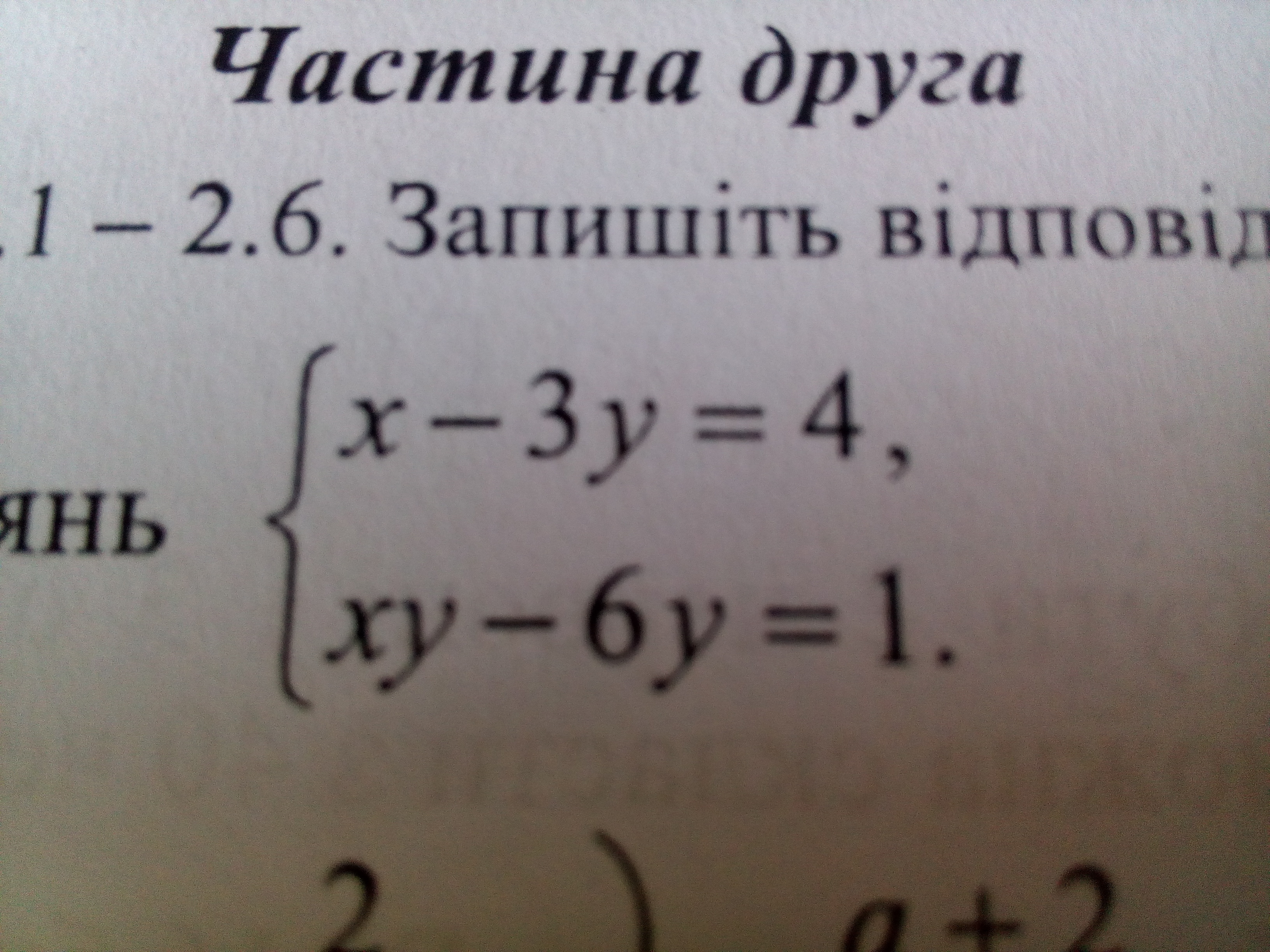
Ответы
Автор ответа:
1
x-3у=4
xy-6y=1
x=4+3y
xy-6y=1
(4+3y)y-6y=1
y=1
y=-1/3
x=4+3*1
x=4+3*(-1/3)
x=7
x=3
х1=7
х2=1
у1=3
у2=-1/3
7-3*1=4
7*1-6*1=1
3-3*(-1/3)=4
3*(-1/3)-6*(-1/3)=1
4=4
1=1
х1=7
у1=1
х2=3
у2=-1/3
xy-6y=1
x=4+3y
xy-6y=1
(4+3y)y-6y=1
y=1
y=-1/3
x=4+3*1
x=4+3*(-1/3)
x=7
x=3
х1=7
х2=1
у1=3
у2=-1/3
7-3*1=4
7*1-6*1=1
3-3*(-1/3)=4
3*(-1/3)-6*(-1/3)=1
4=4
1=1
х1=7
у1=1
х2=3
у2=-1/3
Автор ответа:
1
Решаем подстановкой. Подстановку ищем из 1-го уравнения:
х - 3у = 4, ⇒ х = 4 +3у
Во 2-е уравнение подставим вместо "х" выражение (4 +3у). Получим:
(4 +3у)*у -6у = 1, ⇒ 4у +3у² -6у = 1, ⇒ 3у² -2у -1 = 0. Решаем по "чётному коэффициенту":
х = (1 +-√(1 +3) )/3 = (1 +-2)/3
х₁= 1; х₂ = -1/3
у₁= 4 +3х = 4 +3*1 = 7; у₂ = 4 +3х = 4 +3*1/3 = 4 +1 = 5
Ответ: (1;7); (-1/3; 5)
х - 3у = 4, ⇒ х = 4 +3у
Во 2-е уравнение подставим вместо "х" выражение (4 +3у). Получим:
(4 +3у)*у -6у = 1, ⇒ 4у +3у² -6у = 1, ⇒ 3у² -2у -1 = 0. Решаем по "чётному коэффициенту":
х = (1 +-√(1 +3) )/3 = (1 +-2)/3
х₁= 1; х₂ = -1/3
у₁= 4 +3х = 4 +3*1 = 7; у₂ = 4 +3х = 4 +3*1/3 = 4 +1 = 5
Ответ: (1;7); (-1/3; 5)
Похожие вопросы
Предмет: Русский язык,
автор: sdfghj6323
Предмет: Информатика,
автор: asasindro18
Предмет: Биология,
автор: seidahmatovaeldana
Предмет: История,
автор: raldugina2004
Предмет: Математика,
автор: Flame1234567890