Предмет: Алгебра,
автор: 1albina5
Решите неравенство:
log4 (x+3) + log4 (x+15) ≤ 3
Ответы
Автор ответа:
1
x∈(-3;+∞)
x∈[-19;1]
Ответ :(-3;1]
Автор ответа:
0
Вот так,но не уверена
Приложения:
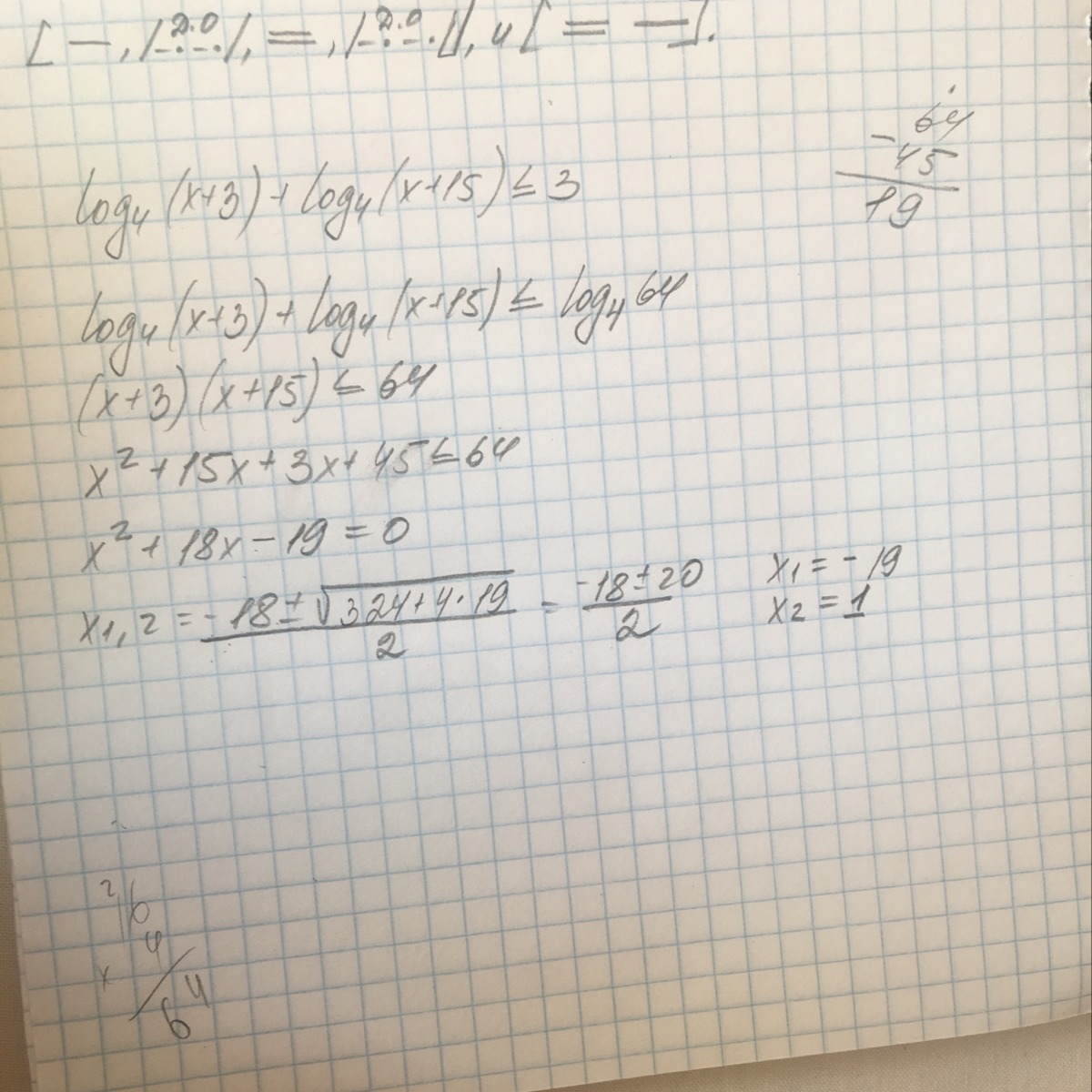
Похожие вопросы
Предмет: Русский язык,
автор: Leam
Предмет: История,
автор: nasty3023
Предмет: Физика,
автор: brihuncovdanil
Предмет: Алгебра,
автор: Магагоча