Предмет: Математика,
автор: rhbrrb
Помогите решить 2 определенных интеграла!! пожалуйста! 9.1.29 и 9.1.31! фото прикреплено
Приложения:
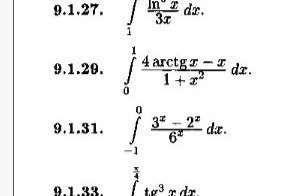
NNNLLL54:
Видно полностью условия только 2-х примеров
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: musanbeibit9
Предмет: Математика,
автор: mrsmolyan
Предмет: Українська література,
автор: Аноним
Предмет: Алгебра,
автор: Ddddas
Предмет: Алгебра,
автор: Ddddas