Исследуйте функцию с помощью производной и постройте ее график:
а) f(x)= 1/2(x+2)(x-2)^2
б) f(x)= x^2-4/x^2+1
в) f(x)= x^2+3x-4/x+1
Ответы
Три исследования функций это очень много. Я напишу одну, остальные делаются точно также.
y= 1/2*(x+2)(x-2)^2
1) Область определения D(x)=R=(-oo; +oo)
2) Разрывов Нет.
Вертикальных асимптот Нет.
3) Четность. Ни четная, ни нечетная.
4) Периодичности Нет.
5) Пересечение с осями.
С осью Oy: x = 0
y(0)=1/2*2(-2)^2=4
С осью Ox: y = 0
x1 = -2; x2 = 2
6) Экстремумы.
y'=1/2*[1*(x-2)^2+(x+2)*2(x-2)]=0
(x-2)(x-2+2(x+2))=0
(x-2)(3x+2)=0
x1=2; y(2)=0 - минимум
x2=-2/3; y(-2/3)=1/2*(4/3)(-8/3)^2=2/3*64/9=128/27 - максимум.
Промежутки возрастания и убывания.
(-oo; -2/3) U (2; +oo) возрастает
(-2/3; 2) убывает.
7) Точки перегиба.
y'' =1/2*[1*(3x+2)+(x-2)*3]=0
3x+2+3x-6=6x-4=0
x=2/3; y(2/3)=1/2*8/3*(-4/3)^2=4/3*16/9=64/27
При x<2/3 график выпуклый вверх.
При x>2/3 график выпуклый вниз.
8) Горизонтальные и наклонные асимптоты.
f(x)=kx+b
k=lim(x->oo) y/x = lim(x->oo) 1/2*(1+2/x)(x-2)^2=1/2*(1+0)(oo)^2=oo
Асимптот нет.
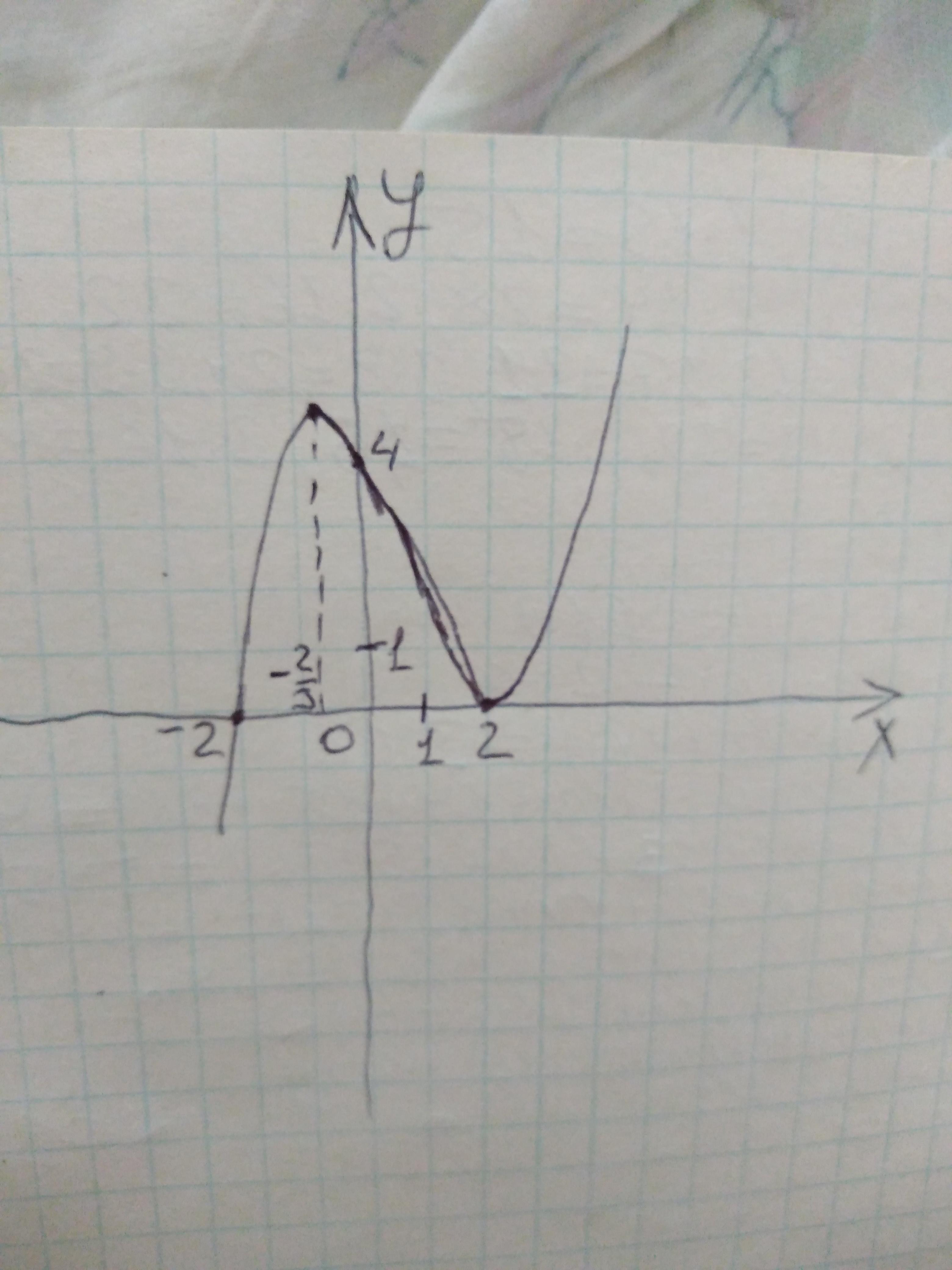
График на рисунке.
2 и 3 функции расписываются точно также, я не буду 3 раза писать одно и тоже.