Предмет: Геометрия,
автор: LordIndorilNerevar
Ребята!! Срочно! В конус, радиус основания которого 6 см и высота 15 см, вписан цилиндр, имеющий наибольшую площадь полной поверхности. Найдите объем цилиндра
Ответы
Автор ответа:
2
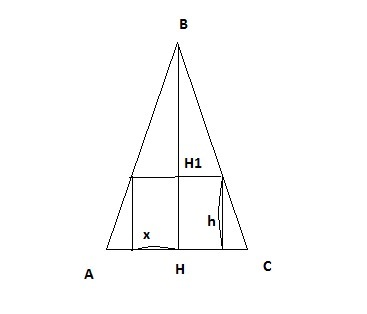
Если рассмотреть сечение, то получится прямоугольник со сторонами 2х и h , вписан в равнобедренный треугольник
Составлю площадь поверхности цилиндра с радиусом х и высотой h (выраженной через х) как функцию от х и через производную найду ее максимум. найденное х подставлю в обем цилиндра...
1) выражу h через х из ΔАВН
tgA=h/(6-x); h=(6-x)*tgA=(6-x)*(15/6)=5(6-x)/2=15-2.5x
S(пов)=2pix^2+2pix*h=2pi*x^2+2pix(15-2.5x)=
=2pix^2+30pix-5pix^2=30pix-3pix^2
приравниваю производную по х к 0
30pi=6pix
x=5 h=5/2=2.5
V=pix^2*h=pi*5^2*2.5=62.5pi
Составлю площадь поверхности цилиндра с радиусом х и высотой h (выраженной через х) как функцию от х и через производную найду ее максимум. найденное х подставлю в обем цилиндра...
1) выражу h через х из ΔАВН
tgA=h/(6-x); h=(6-x)*tgA=(6-x)*(15/6)=5(6-x)/2=15-2.5x
S(пов)=2pix^2+2pix*h=2pi*x^2+2pix(15-2.5x)=
=2pix^2+30pix-5pix^2=30pix-3pix^2
приравниваю производную по х к 0
30pi=6pix
x=5 h=5/2=2.5
V=pix^2*h=pi*5^2*2.5=62.5pi
Приложения:
Похожие вопросы
Предмет: Математика,
автор: daraalemaeva0
Предмет: История,
автор: Andrei121222
Предмет: История,
автор: dornova98
Предмет: Математика,
автор: evelonis