Предмет: Математика,
автор: sokolova20001
Здравствуйте. Помогите решить примеры по тригонометрии. Если вы знаете решение хотя бы на 1, то напишите.
Приложения:
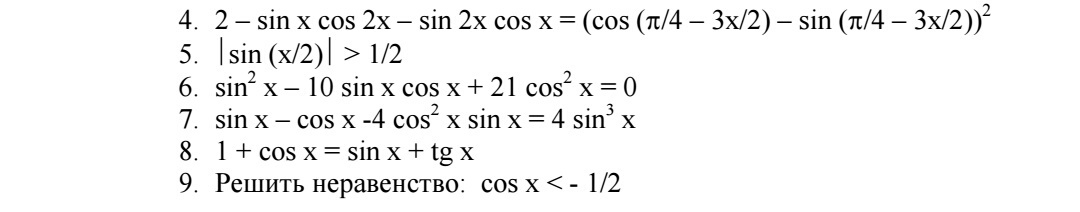
Ответы
Автор ответа:
2
4. 2-sin x*cos 2x-sin 2x*cos x = (cos(Π/4-3x/2)-sin(Π/4-3x/2))^2
Решаем по действиям
1) sin x*cos 2x + cos x*sin 2x = sin(x+2x) = sin 3x
2) (cos(Π/4-3x/2)-sin(Π/4-3x/2))^2 = cos^2(Π/4-3x/2)+sin^2(Π/4-3x/2)-2cos(Π/4-3x/2)*sin(Π/4-3x/2)=
= 1 - sin(Π/2-3x) = 1 - cos 3x
Подставляем
2-sin 3x = 1-cos 3x
sin 3x - cos 3x = 1
Преобразуем так:
√2*(1/√2*sin 3x - 1/√2*cos 3x) = 1
-√2*(cos 3x*cos Π/4 - sin 3x*sin Π/4) = 1
-√2*cos(3x+Π/4) = 1
cos(3x+Π/4) = -1/√2
3x1 + Π/4 = 3Π/4 + 2Π*k; x1 = Π/6+2Π/3*k
3x2 + Π/4 = 5Π/4 + 2Π*k; x2 = Π/3 + 2Π/3*k
5. |sin(x/2)| > 1/2
1) sin(x/2) < -1/2
x/2 € (-5Π/6+2Π*k; -Π/6+2Π*k)
x1 € (-5Π/3+4Π*k; -Π/3+4Π*k)
2) sin(x/2) > 1/2
x/2 € (Π/6+2Π*k; 5Π/6+2Π*k)
x2 € (Π/3+4Π*k; 5Π/3+4Π*k)
6) sin^2 x - 10sin x*cos x + 21cos^2 x = 0
Делим всё на cos^2 x
tg^2 x - 10tg x + 21 = 0
(tg x - 3)(tg x - 7) = 0
1) tg x = 3; x1 = arctg 3 + Π*k
2) tg x = 7; x2 = arctg 7 + Π*k
7) sin x - cos x - 4cos^2 x*sin x = 4sin^3 x
sin x - cos x = 4sin^3 x + 4cos^2 x*sin x
sin x - cos x = 4sin x*(sin^2 x + cos^2 x) = 4sin x
3sin x = -cos x
tg x = -1/3
x = -arctg(1/3) + Π*k
8) 1 + cos x = sin x + tg x = sin x + sin x/cos x
Умножаем всё на cos x
cos x*(1+cos x) = sin x*cos x + sin x
cos x*(1+cos x) - sin x*(1+cos x) = 0
(1+cos x)(cos x - sin x) = 0
1) cos x = -1; x1 = Π+2Π*k
2) cos x = sin x
tg x = 1; x2 = Π/4+Π*k
9) cos x < -1/2
x € (2Π/3+2Π*k; 4Π/3+2Π*k)
Решаем по действиям
1) sin x*cos 2x + cos x*sin 2x = sin(x+2x) = sin 3x
2) (cos(Π/4-3x/2)-sin(Π/4-3x/2))^2 = cos^2(Π/4-3x/2)+sin^2(Π/4-3x/2)-2cos(Π/4-3x/2)*sin(Π/4-3x/2)=
= 1 - sin(Π/2-3x) = 1 - cos 3x
Подставляем
2-sin 3x = 1-cos 3x
sin 3x - cos 3x = 1
Преобразуем так:
√2*(1/√2*sin 3x - 1/√2*cos 3x) = 1
-√2*(cos 3x*cos Π/4 - sin 3x*sin Π/4) = 1
-√2*cos(3x+Π/4) = 1
cos(3x+Π/4) = -1/√2
3x1 + Π/4 = 3Π/4 + 2Π*k; x1 = Π/6+2Π/3*k
3x2 + Π/4 = 5Π/4 + 2Π*k; x2 = Π/3 + 2Π/3*k
5. |sin(x/2)| > 1/2
1) sin(x/2) < -1/2
x/2 € (-5Π/6+2Π*k; -Π/6+2Π*k)
x1 € (-5Π/3+4Π*k; -Π/3+4Π*k)
2) sin(x/2) > 1/2
x/2 € (Π/6+2Π*k; 5Π/6+2Π*k)
x2 € (Π/3+4Π*k; 5Π/3+4Π*k)
6) sin^2 x - 10sin x*cos x + 21cos^2 x = 0
Делим всё на cos^2 x
tg^2 x - 10tg x + 21 = 0
(tg x - 3)(tg x - 7) = 0
1) tg x = 3; x1 = arctg 3 + Π*k
2) tg x = 7; x2 = arctg 7 + Π*k
7) sin x - cos x - 4cos^2 x*sin x = 4sin^3 x
sin x - cos x = 4sin^3 x + 4cos^2 x*sin x
sin x - cos x = 4sin x*(sin^2 x + cos^2 x) = 4sin x
3sin x = -cos x
tg x = -1/3
x = -arctg(1/3) + Π*k
8) 1 + cos x = sin x + tg x = sin x + sin x/cos x
Умножаем всё на cos x
cos x*(1+cos x) = sin x*cos x + sin x
cos x*(1+cos x) - sin x*(1+cos x) = 0
(1+cos x)(cos x - sin x) = 0
1) cos x = -1; x1 = Π+2Π*k
2) cos x = sin x
tg x = 1; x2 = Π/4+Π*k
9) cos x < -1/2
x € (2Π/3+2Π*k; 4Π/3+2Π*k)
Похожие вопросы
Предмет: Литература,
автор: slimebyilya
Предмет: Математика,
автор: semensemenovic107
Предмет: Геометрия,
автор: otpicatokinetolkootp
Предмет: Математика,
автор: svetochkababae
Предмет: Математика,
автор: ОмЛ9т