Предмет: Алгебра,
автор: вика2112
Решить интеграл методом замены переменной
Приложения:

Ответы
Автор ответа:
1
Приложения:
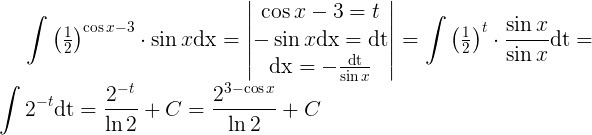
Похожие вопросы
Предмет: История,
автор: xxxxxxxxxxx0000003
Предмет: Українська література,
автор: anastasiy804
Предмет: Алгебра,
автор: melonaaa
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: vitalik9739hxh