Предмет: Математика,
автор: anastasiasavcen
ПОМОГИТЕ ПОЖАЛУЙСТА НАЙТИ ВТОРУЮ ПРОИЗВОДНУЮ! СРОЧНО НАДО
Приложения:

moboqe:
всех функции?
да
я надеюсь решишь
Ответы
Автор ответа:
0
Приложения:
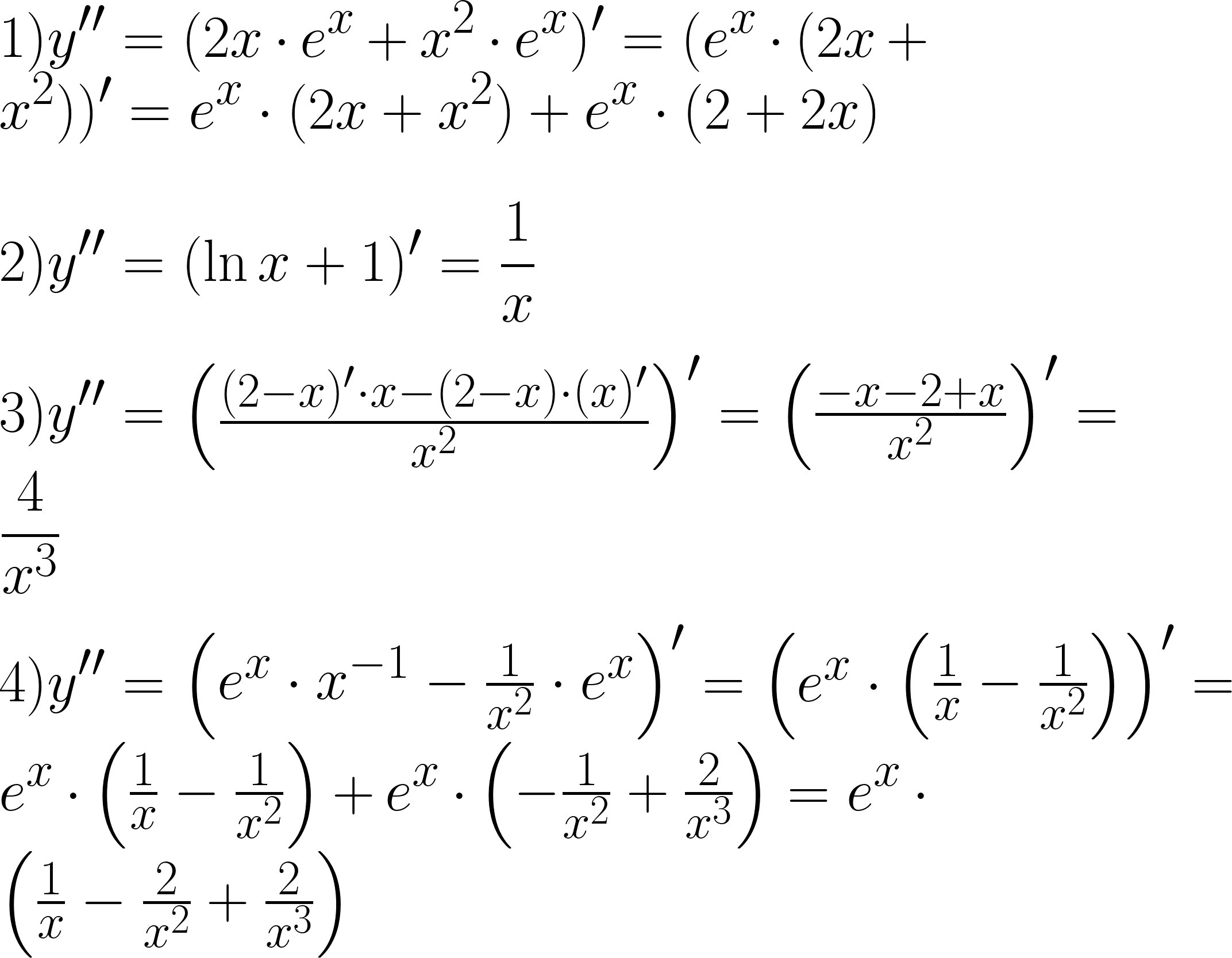
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: AaEeAaEe
Предмет: Алгебра,
автор: achkasovaolga2007
Предмет: Математика,
автор: dimich10