Предмет: Геометрия,
автор: unique00
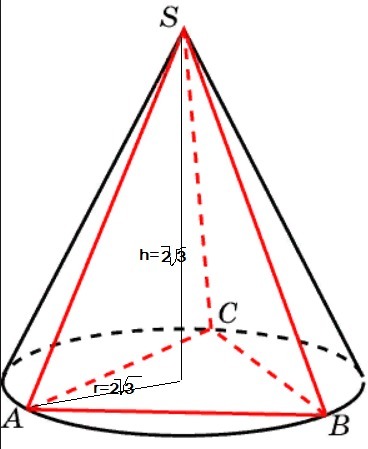
Правильная треугольная пирамида вписана в конус радиус основания которого равна высоте и составляет 2√3. Найдите объем пирамиды.
Ответы
Автор ответа:
1
V пир=1/3*S*h, где S-площадь основания пирамиды, h-высота пирамиды.
В основании по условию лежит равносторонний треугольник, вписанный в окружность ⇒
S=(3√3/4)*R², где R-радиус описанной окружности.
S=(3√3/4)*(2√3)²=9√3.
V пир=1/3*S*h=9√3*2√3/3=18
В основании по условию лежит равносторонний треугольник, вписанный в окружность ⇒
S=(3√3/4)*R², где R-радиус описанной окружности.
S=(3√3/4)*(2√3)²=9√3.
V пир=1/3*S*h=9√3*2√3/3=18
Приложения:
unique00:
а почему когда ищем площу то 3√3/4 в формуле ж √3/4??? √-это корень
и когда ищем обьем то 2√3/3? почему делим на 3?
там надо читать не корень из трех четвертых, а корень из трех, деленное на 4
да я знаю, а почему там 3 спереди?
я не понимаю-где спереди? Откройте учебник, найдете формулу для площади равностороннего треугольника через радиус описанной окружности. Это она: S=(3√3/4)*R²
Похожие вопросы
Предмет: Английский язык,
автор: Manapovazhan
Предмет: Математика,
автор: sky923pro
Предмет: Алгебра,
автор: svyatoslav81u
Предмет: Математика,
автор: марина2468