Предмет: Математика,
автор: afanasevanatal
100 баллов!!!
решите!!!
Приложения:

Ответы
Автор ответа:
0
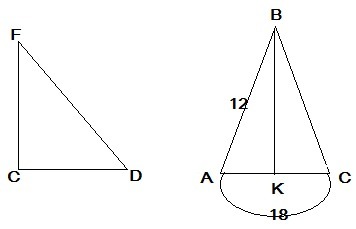
1. Нарисуем треугольник, подпишем углы: в нашем треугольнике FC, CD-катеты, FD- гипотенуза.
cos F=FC/FD (косинус острого угла в прямоугольном треугольнике - это отношение прилежащего катета к гипотенузе),
sin D=FC/FD (синус острого угла в прямоугольном треугольнике-это отношение противолежащего катета к гипотенузе)⇒
sin D=cos F=0,4
2.Опустим высоту ВК. В равнобедренном треугольнике высота является также медианой, поэтому AK=AC/2=18/2=9.
Найдем cosA.
cosA=AK/AB ⇒
cosA=9/12=3/4
cos F=FC/FD (косинус острого угла в прямоугольном треугольнике - это отношение прилежащего катета к гипотенузе),
sin D=FC/FD (синус острого угла в прямоугольном треугольнике-это отношение противолежащего катета к гипотенузе)⇒
sin D=cos F=0,4
2.Опустим высоту ВК. В равнобедренном треугольнике высота является также медианой, поэтому AK=AC/2=18/2=9.
Найдем cosA.
cosA=AK/AB ⇒
cosA=9/12=3/4
Приложения:
Автор ответа:
0
1) ∠F=90°-∠D
cos∠F=cos(90°-∠D)=sin∠D=0,4

cos∠F=cos(90°-∠D)=sin∠D=0,4
Похожие вопросы
Предмет: Английский язык,
автор: Manapovazhan
Предмет: Математика,
автор: sky923pro
Предмет: Алгебра,
автор: svyatoslav81u
Предмет: Математика,
автор: PACAN13371337
Предмет: Математика,
автор: математика374