Предмет: Алгебра,
автор: Вовина79
\sqrt{3} tg(\frac{\pi}{3}-x)-1\leq 0
Ответы
Автор ответа:
0
Приложения:
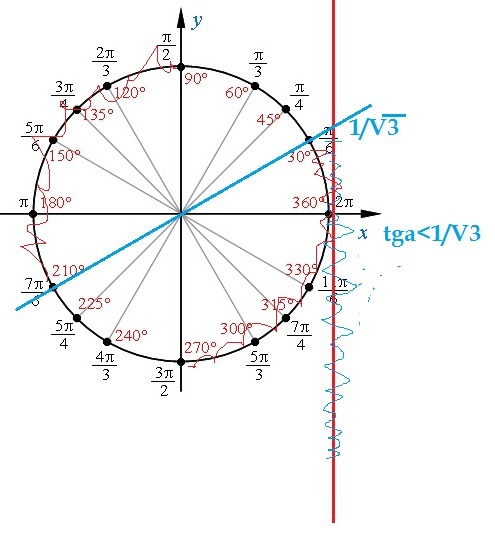
Похожие вопросы
Предмет: Математика,
автор: tatyana5384
Предмет: Математика,
автор: denisdrobot93
Предмет: Химия,
автор: Beyon1
Предмет: Математика,
автор: tutsy2005
Предмет: Математика,
автор: Амина7711