Предмет: Алгебра,
автор: morozov7p
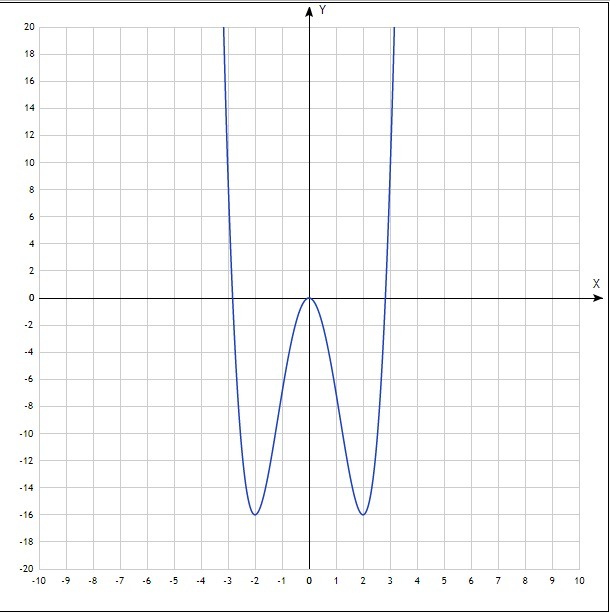
исследовать график функции y=x^4-8x^2
Ответы
Автор ответа:
0
пересечение с Оу:
х=0
у=0
(0;0)
пересечение с Ох:
у=0
График в файле..
Приложения:
Похожие вопросы
Предмет: Математика,
автор: fazof2005
Предмет: Другие предметы,
автор: Аноним
Предмет: Химия,
автор: georgijkanila582
Предмет: История,
автор: skatovav02
Предмет: Математика,
автор: Natali2407