Предмет: Геометрия,
автор: AquAlexa
Нужна задача №6 только, с чертежом.
Дано: ABCD - квадрат. Точка М лежит вне плоскости ABC. Найти расстояние между прямыми AМ и BD.
Приложения:
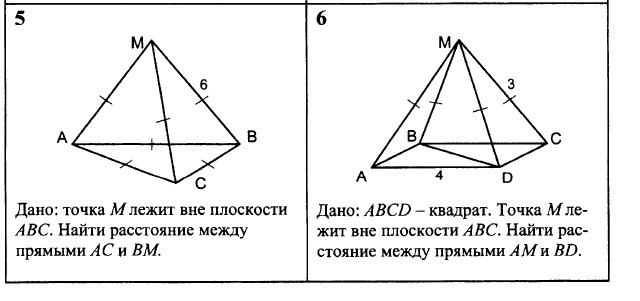
Ответы
Автор ответа:
9
Пусть E - проекция точки M на плоскость ABC
 - диагональ квадрата со стороной 4
- диагональ квадрата со стороной 4
 - половина диагонали, т.к. треугольник BMD равнобедренный и высота делит основание пополам
- половина диагонали, т.к. треугольник BMD равнобедренный и высота делит основание пополам
 - по той же причине
- по той же причине
 - теорема Пифагора
- теорема Пифагора
Теперь рассмотрим треугольник АМЕ. Угол AEM - прямой, т.к. E=проекция K на плоскость основания
Пусть К - проекция точки E на прямую AM. Т.е. EKM - прямой.
Вспомним, что синус угла - отношение противолежащего катета к гипотенузе, тогда

Ответ:
Теперь рассмотрим треугольник АМЕ. Угол AEM - прямой, т.к. E=проекция K на плоскость основания
Пусть К - проекция точки E на прямую AM. Т.е. EKM - прямой.
Вспомним, что синус угла - отношение противолежащего катета к гипотенузе, тогда
Ответ:
Приложения:
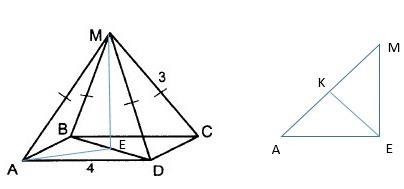
AquAlexa:
Спасибо!!!
Похожие вопросы
Предмет: Биология,
автор: ali8932
Предмет: Математика,
автор: ilasushkov763
Предмет: Русский язык,
автор: maksatakimov475
Предмет: Литература,
автор: Polya310306Maltseva