Question

В треугольнике АБС проведена биссектриса БК. Докажите, что АК:СК=БА:СБ

Answer 1

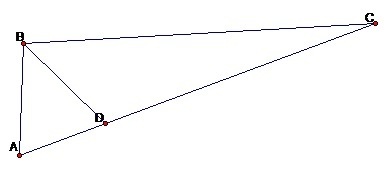
На рисунке обозначения другие.
 Несколько способов существует. Докажем через отношение площадей.
 Треугольники имеют общую вершину, их площади относятся как их основания:  S(ABD) : S(DBC) =  AD : DC.
 У этих треугольников равные углы, поэтому отношение площадей равно отношению произведений сторон, образующих эти равные углы.
S(ABD) : S(DBC) =  (AB*BD) :( BD*BC) = AB : BC.
И получаем  AD: DC = AB:BC).