Предмет: Геометрия,
автор: Dashkova2018
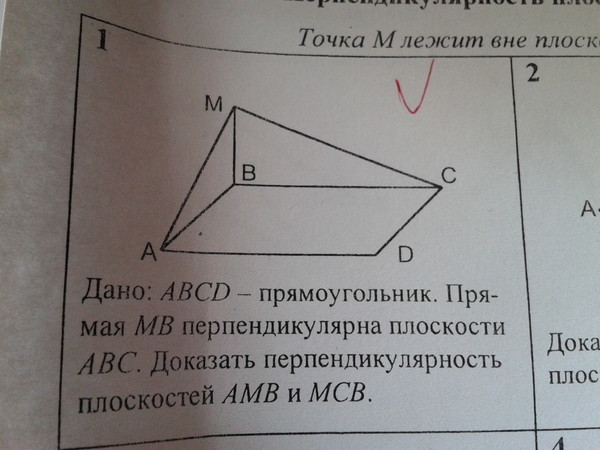
1)Дано: ABCD - прямоугольник. Прямая MB перпендикулярна плоскости ABC. Доказать перпендикулярность плоскостей AMB и MCB.
Приложения:
Ответы
Автор ответа:
7
Плоскости перпендикулярны, если угол между ними - прямой. Угол между плоскостями (двугранный угол) измеряется меньшим линейным углом, т. е. меньшим углом между перпендикулярами в плоскостях к точке на прямой, по которой плоскости пересекаются.
Прямая MB перпендикулярна ABC и по определению перпендикулярна любой прямой в этой плоскости. Прямые AB и BC лежат в плоскости ABC, следовательно перпендикулярны MB.
Плоскости AMB и MCB пересекаются по прямой MB. Прямые AB и BC лежат в плоскостях AMB и MCB и являются перпендикулярами к точке на MB, следовательно угол между AB и BC определяет угол между плоскостями AMB и MCB. Угол между AB и BC - прямой (ABCD - прямоугольник, все углы прямые), плоскости AMB и MCB - перпендикулярны.
Прямая MB перпендикулярна ABC и по определению перпендикулярна любой прямой в этой плоскости. Прямые AB и BC лежат в плоскости ABC, следовательно перпендикулярны MB.
Плоскости AMB и MCB пересекаются по прямой MB. Прямые AB и BC лежат в плоскостях AMB и MCB и являются перпендикулярами к точке на MB, следовательно угол между AB и BC определяет угол между плоскостями AMB и MCB. Угол между AB и BC - прямой (ABCD - прямоугольник, все углы прямые), плоскости AMB и MCB - перпендикулярны.
Похожие вопросы
Предмет: Алгебра,
автор: yakovlyevadiana
Предмет: Математика,
автор: turysovnikolaj
Предмет: Физика,
автор: Iren245
Предмет: Физика,
автор: kossok