Найдите наибольшее и наименьшее значение функции f(x)=x^4-2x^2+3
На отрезке [-4;3]
Ответы
Ответ:
f min = 2, f max = 227
Объяснение:
f(x)=x⁴-2x²+3
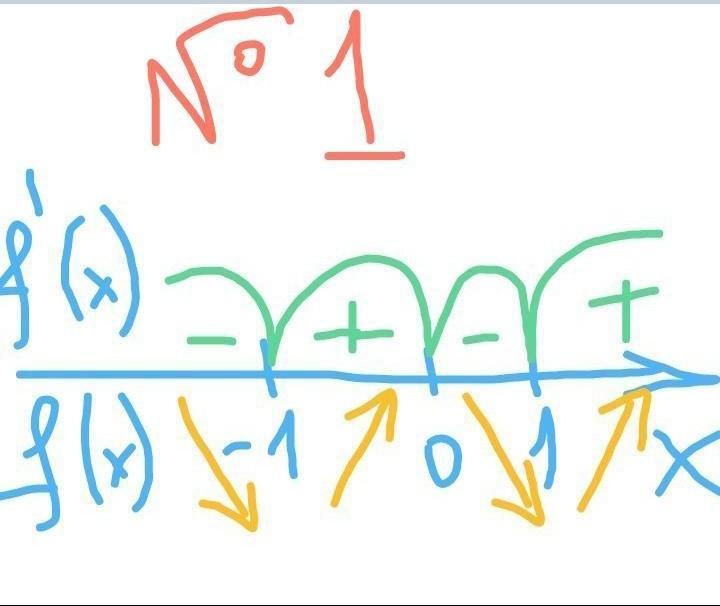
находим производную:
f'=(х⁴-2x²+3)'=4х³-2*2х+0= 4х³-4х
приравниваем производные к 0:
f' = 4x³-4x=0
находим критические точки:
4x³-4x=0
4х(х²-1)=0
4х(х-1)(х+1)=0
х=0 или х-1=0 или х+1=0
х1=0, х2=1, х3=-1
смотри прикрепленное изображение 1
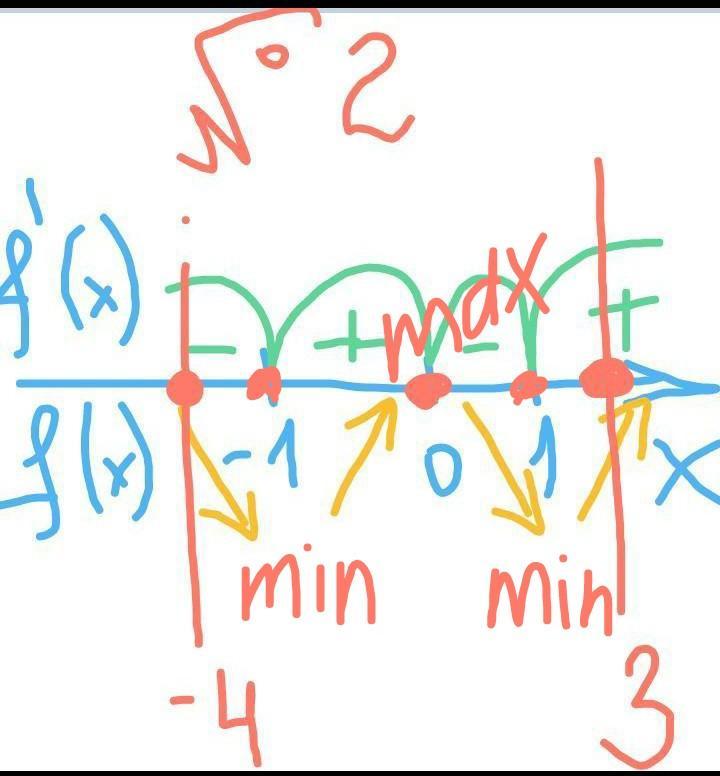
необходимо найти наибольшее и наименьшее значение на промежутке [-4;3]
(прикрепленное изображение 2)
Для нахождения наибольшего и наименьшего значения функции на заданном отрезке достаточно вычислить её значения на концах отрезка ( х=-4 и х=3 ), в точке максимума (х=0) и точках минимума (х=-1 и х=1).
f(x)=x⁴-2x²+3 →
Эти значения функции:
f(-4)=(-4)⁴-2*(-4)²+3=256-32+3=227
f(-1)=(-1)⁴-2*(-1)²+3=1-2+3=2
f(0)=0⁴-2*(0)²+3=0-0+3=3
f(1)=(1)⁴-2*(1)²+3=1-2+3=2
f(3)=(3)⁴-2*(3)²+3=81-18+3=66 →
Наименьшее значение функции в точках х=-1 и х=1 и f(x)=2,
а наибольшее значение функции в точке х=-4 и f(x)=227