Предмет: Математика,
автор: evaava098
(x^2+x+1)^x < 1 Подробно если можно :)
Приложения:
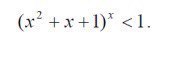
Ответы
Автор ответа:
1
рассмотрим два случая
1) если выражение под скобками будет меньше 1,то степень должна быть положительной,то есть больше нуля.
решим это систему неравенств
x²+x+1<1
находим нули функции,то есть решим квадратное ур-е и найдем его корни
x1=-1 x2=0
далее методом интервалов
+ - +
..................-1............0...............,смотрим какие значение принимает фун-я в каждом промежутке
нас интересовало меньше нули,значит (-1;0),решением воторого не-ва будет (0;+∞)
теперь объединяем оба решения на одной числовой прямой,если совпадают ,то это и будет интересующий нас промежуток
решение первого неравенства (-1;0),общих промежутков у 2-х неравенств нет,значит этот вариант не подходит
2)теперь рассмотрим вариант ,если выражение под скобками будет больше 1,тогда степень должна быть меньше 0

решением этой системы будет промежуток (-∞;1) это и будет ответ
1) если выражение под скобками будет меньше 1,то степень должна быть положительной,то есть больше нуля.
решим это систему неравенств
x²+x+1<1
находим нули функции,то есть решим квадратное ур-е и найдем его корни
x1=-1 x2=0
далее методом интервалов
+ - +
..................-1............0...............,смотрим какие значение принимает фун-я в каждом промежутке
нас интересовало меньше нули,значит (-1;0),решением воторого не-ва будет (0;+∞)
теперь объединяем оба решения на одной числовой прямой,если совпадают ,то это и будет интересующий нас промежуток
решение первого неравенства (-1;0),общих промежутков у 2-х неравенств нет,значит этот вариант не подходит
2)теперь рассмотрим вариант ,если выражение под скобками будет больше 1,тогда степень должна быть меньше 0
решением этой системы будет промежуток (-∞;1) это и будет ответ
evaava098:
напишите как "решим эту систему неравенств" пожалуйста
Похожие вопросы
Предмет: Физика,
автор: dakovleva772
Предмет: Алгебра,
автор: abultimur455
Предмет: Математика,
автор: karoliukas042
Предмет: Математика,
автор: alionaivanova21
Предмет: Математика,
автор: lenai76