Question

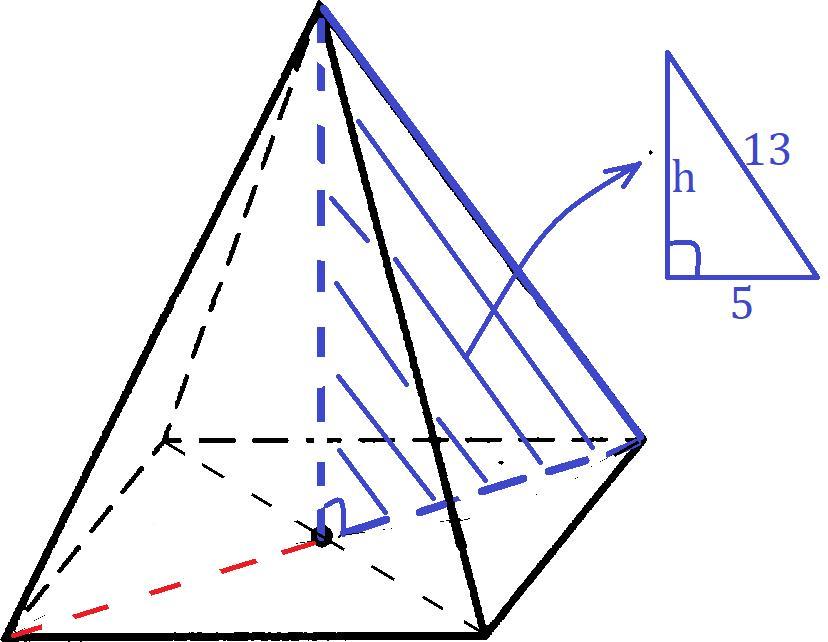
диагональ основания правильной четырехугольной пирамиды равна 10, а боковое ребро равно 13. Найдите высоту пирамиды

Answer 1

Высота правильной пирамиды падает в центр основания. В основании лежит правильный n-угольник, в нашем случаи n=4, то есть это квадрат. Центр квадрата лежит на пересечении его диагоналей. Диагонали делятся точкой пересечения пополам.

Рассмотрим прямоугольный треугольник гипотенуза которого является боковым ребром пирамиды, а катет - высотой (h) пирамиды. Другой катет равен 10:2=5 (половина диагонали квадрата). Гипотенуза равна 13. По пифагоровой тройке h=12. Ну или по теореме Пифагора:

$\displaystyle h=\sqrt{13^2-5^2} =\sqrt{(13-5)(13+5)} =\sqrt{4^2\cdot 3^2} =12$

Ответ: 12.