Предмет: Алгебра,
автор: helpmeplz000
Выделить полный квадрат
Приложения:
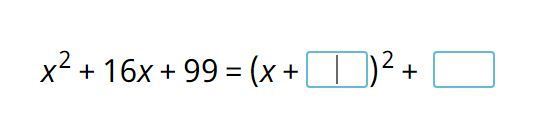
Ответы
Автор ответа:
0
Чтобы выражение было полным квадратом, необходимо, чтобы дискриминант квадратного уравнения был равен нулю, тогда будет два совпадающих корня, который при разложении многочлена на множители (ax² + bx + c = a(x - x1)(x - x2)) и даст полный квадрат. Тогда давайте попробуем посмотреть, как надо разложить свободный член 99, чтобы из оставшегося выражения получился полный квадрат. Итак, попробуем разложить на множители данное выражение, для этого решим уравнение:
x² + 16x + 99 = 0
Нужно, чтобы D был равен нулю, то есть мы должны разложить 99.
D = 16² - 4 · с = 256 - 4с (где с – какое-то число, которое мы возьмем для получения полного квадрата).
D = 0, тогда 256 = 4с, с = 64.
Тогда исходное выражение представим в виде
x² +16x + 64 + 35 = 0
Разложим на множители x² + 16x + 64: корень = -16/2 = -8. 35 просто остается.
По уже упомянутой выше формуле разложения многочлена на множители, получим
(x + 8)² + 35
То есть x² + 16x + 99 = (x + 8)² + 35.
x² + 16x + 99 = 0
Нужно, чтобы D был равен нулю, то есть мы должны разложить 99.
D = 16² - 4 · с = 256 - 4с (где с – какое-то число, которое мы возьмем для получения полного квадрата).
D = 0, тогда 256 = 4с, с = 64.
Тогда исходное выражение представим в виде
x² +16x + 64 + 35 = 0
Разложим на множители x² + 16x + 64: корень = -16/2 = -8. 35 просто остается.
По уже упомянутой выше формуле разложения многочлена на множители, получим
(x + 8)² + 35
То есть x² + 16x + 99 = (x + 8)² + 35.
Похожие вопросы
Предмет: Геометрия,
автор: kristinapekar
Предмет: Литература,
автор: naruto5677
Предмет: Геометрия,
автор: ocatmyl
Предмет: Химия,
автор: MariyaKykolka
Предмет: Алгебра,
автор: schkOOOlnik