Предмет: Математика,
автор: Boomm7771
Срочно. 3 номера всего нужно. Любых
Приложения:
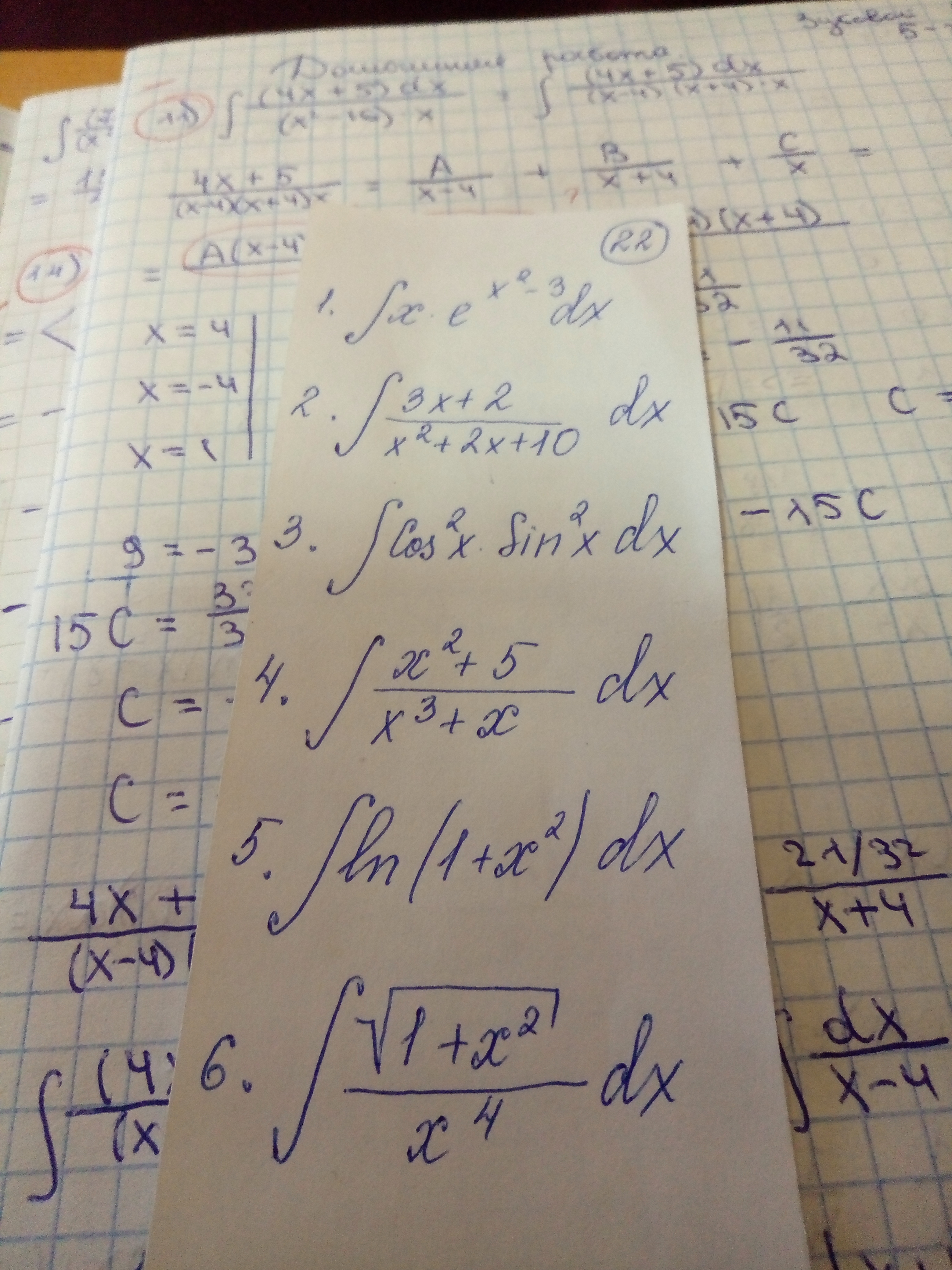
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: wer123578
Предмет: Химия,
автор: 076435wqrub
Предмет: Химия,
автор: aikanishbaimatova7
Предмет: Алгебра,
автор: Аноним
Предмет: Физика,
автор: simba2304