Предмет: Алгебра,
автор: Vikins00
Решить с объяснением
Приложения:
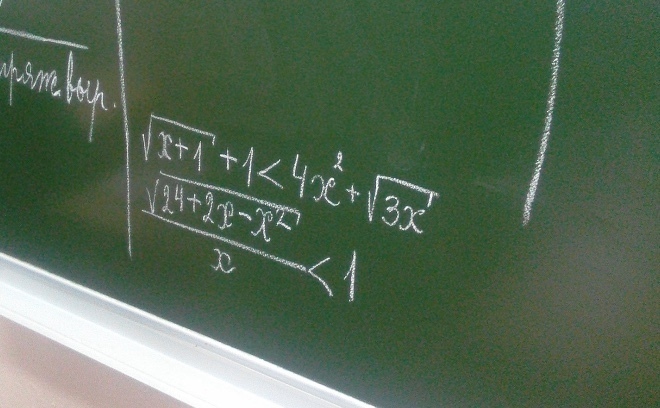
Аноним:
только 2-е могу. надо?
Ответы
Автор ответа:
1
1) ОДЗ:  Подстановкой в неравенство убеждаемся, что x=0 решением не является. Пусть x>0. Поделим неравенство на
Подстановкой в неравенство убеждаемся, что x=0 решением не является. Пусть x>0. Поделим неравенство на 

Замечаем, что левая часть убывает, а правая возрастает. Поэтому нужно угадать x, при котором неравенство превращается в равенство, и в ответ написать все, что лежит правее. Процесс угадывания не очень прост, но приводит к
Ответ:
2) ОДЗ:
![x\in [-4;0)\cup (0;6] x\in [-4;0)\cup (0;6]](https://tex.z-dn.net/?f=x%5Cin+%5B-4%3B0%29%5Ccup+%280%3B6%5D)
1-й случай. левая часть меньше либо равна 0 и поэтому неравенство выполнено.
левая часть меньше либо равна 0 и поэтому неравенство выполнено.
2-й случай.![x\in (0;6] x\in (0;6]](https://tex.z-dn.net/?f=x%5Cin+%280%3B6%5D) ; занесем x, стоящий в знаменателе, под знак корня:
; занесем x, стоящий в знаменателе, под знак корня:

Левая часть убывает, правая постоянна. Поэтому достаточно выяснить, когда левая и правая части совпадают, и взять все, что стоит справа. Если угадать x=4 представляется очень сложным, можно просто решить уравнение (но при этом задача теряет свой шарм)

положительный корень x=4.
Ответ:![[-4;0)\cup (4;6] [-4;0)\cup (4;6]](https://tex.z-dn.net/?f=%5B-4%3B0%29%5Ccup+%284%3B6%5D)
Замечаем, что левая часть убывает, а правая возрастает. Поэтому нужно угадать x, при котором неравенство превращается в равенство, и в ответ написать все, что лежит правее. Процесс угадывания не очень прост, но приводит к
Ответ:
2) ОДЗ:
1-й случай.
2-й случай.
Левая часть убывает, правая постоянна. Поэтому достаточно выяснить, когда левая и правая части совпадают, и взять все, что стоит справа. Если угадать x=4 представляется очень сложным, можно просто решить уравнение (но при этом задача теряет свой шарм)
положительный корень x=4.
Ответ:
Автор ответа:
1
Фотофотофотофотофото
Приложения:

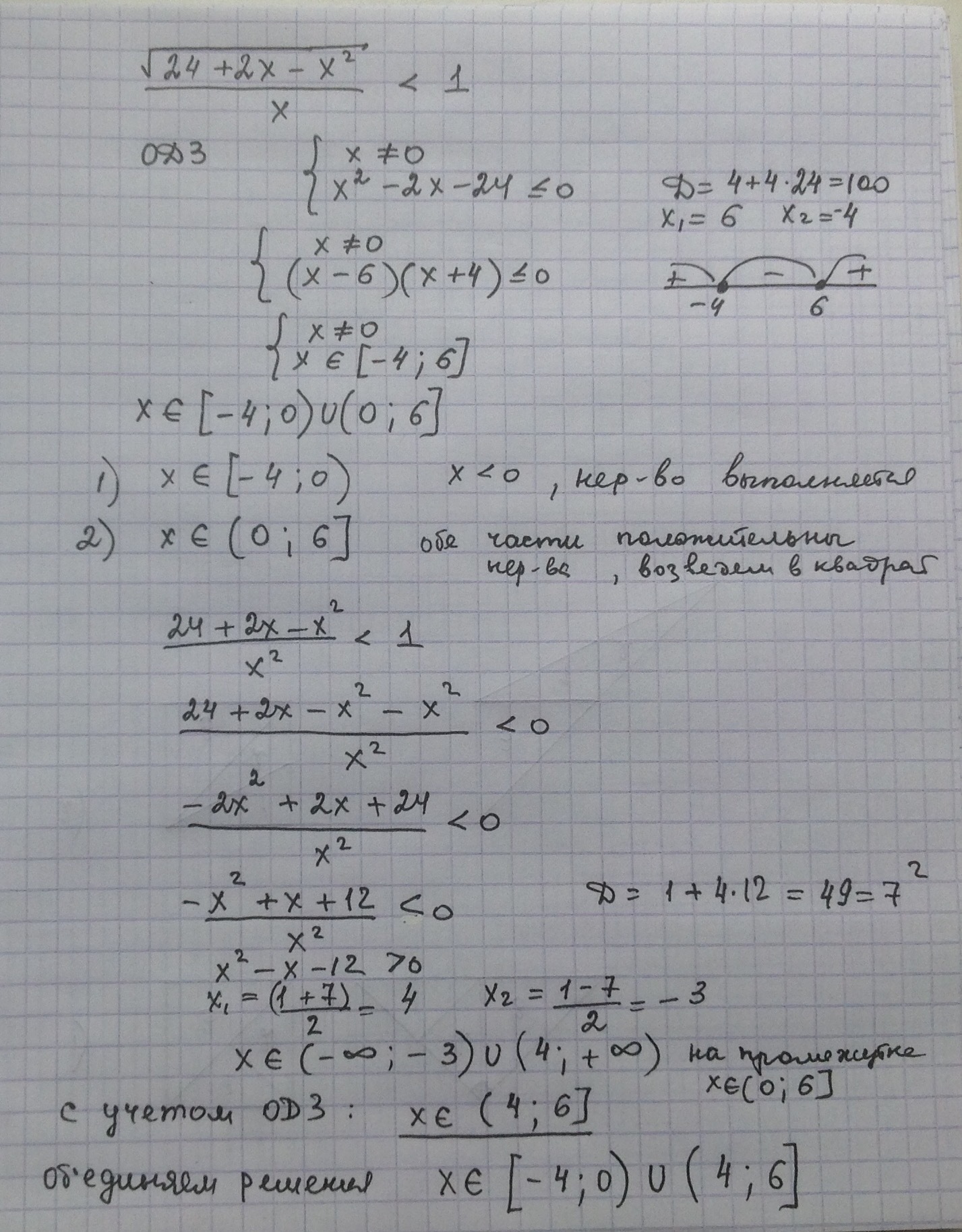
Похожие вопросы
Предмет: Математика,
автор: kravcenkom234
Предмет: Математика,
автор: ftagieva844
Предмет: Немецкий язык,
автор: vhbj55
Предмет: География,
автор: 89587169391
Предмет: Математика,
автор: ававав3