Предмет: Геометрия,
автор: girlsanime
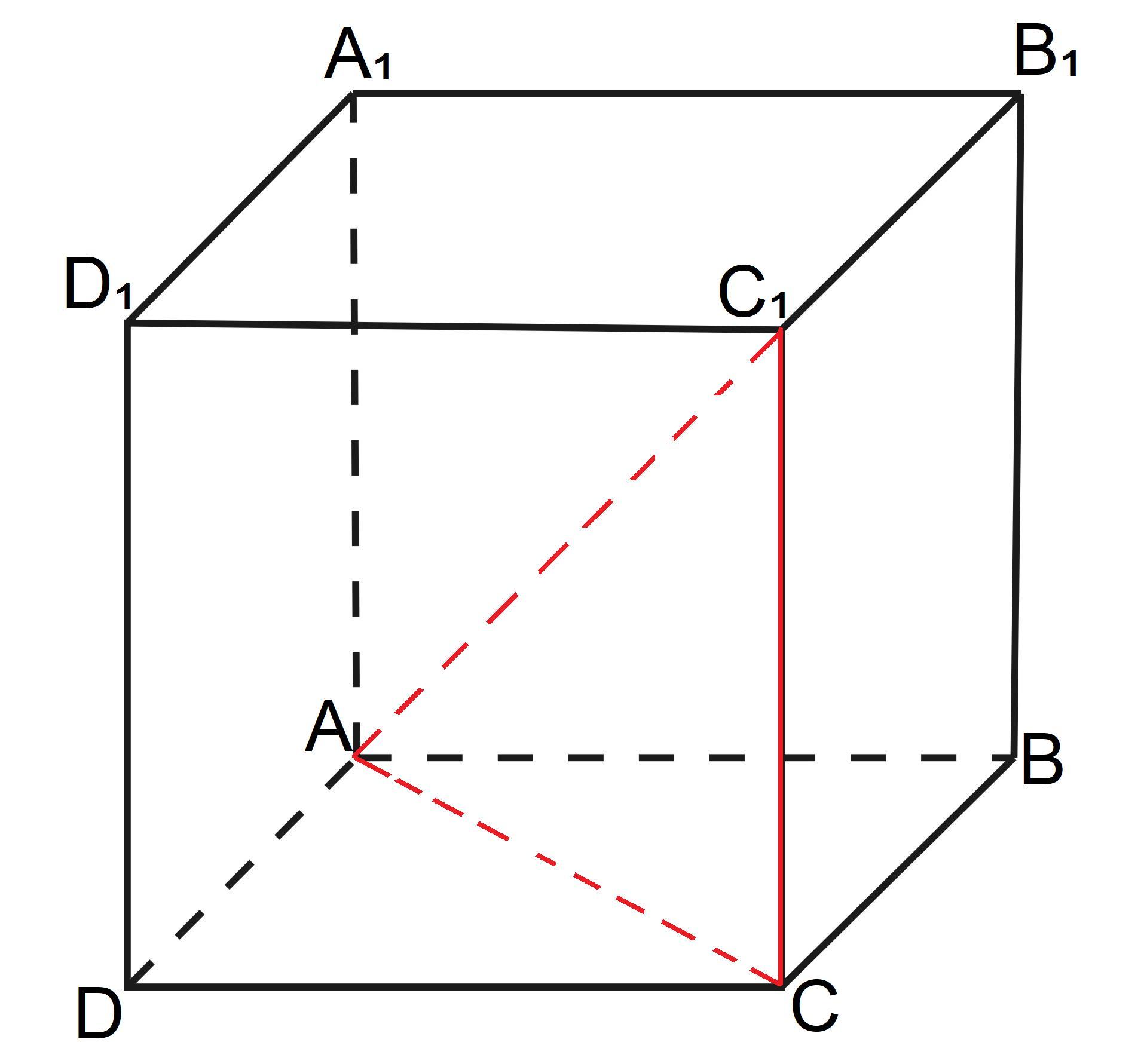
Задача ABCDA1B1C1D1- куб. Докажите, что плоскость треугольника АСС1 проходит через точку А1.
Ответы
Автор ответа:
0
AA₁ и CC₁ ⊥ (ABC) как рёбра куба.
Поэтому AA₁║CC₁
AA₁║CC₁ ⊂ (ACC₁), поэтому AA₁║(ACC₁) или AA₁ ⊂ (ACC₁). A ∈ AA₁, (ACC₁) значит, AA₁ не может быть параллельной плоскости (ACC₁) (одна общая точка уже есть). Осталось одно возможно взаимное расположение в пространстве: AA₁ ⊂ (ACC₁). А значит, любая точка прямой AA₁ принадлежит плоскости (ACC₁): A∈AA₁⊂(ACC₁) ⇒ A₁∈(ACC₁).
Иными словами, плоскость (ACC₁) проходит через точку A₁ , что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: rodiontsevaau
Предмет: Английский язык,
автор: lysyakova200740
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: водила