Question

Ради бога помогите с этой задачью)В правильной четырёхугольной пирамиде, длина
диагонали основания равна 2√2 см, а длина высоты
равна 3 см. Найдите объем пирамиды.

Answer 1

по т.Пифагора диагональ квадрата равна d=a²+a²=2a²  откуда а²=d:2,но площадь квадрата со стороной а тоже равна S=a²,тогда S=d:2=(2√2):2=√2cм²          Н=3 см
V=1\3 Sосн*H=1\3*√2*3=√2 см³

Answer 2

РЕШЕНИЕ
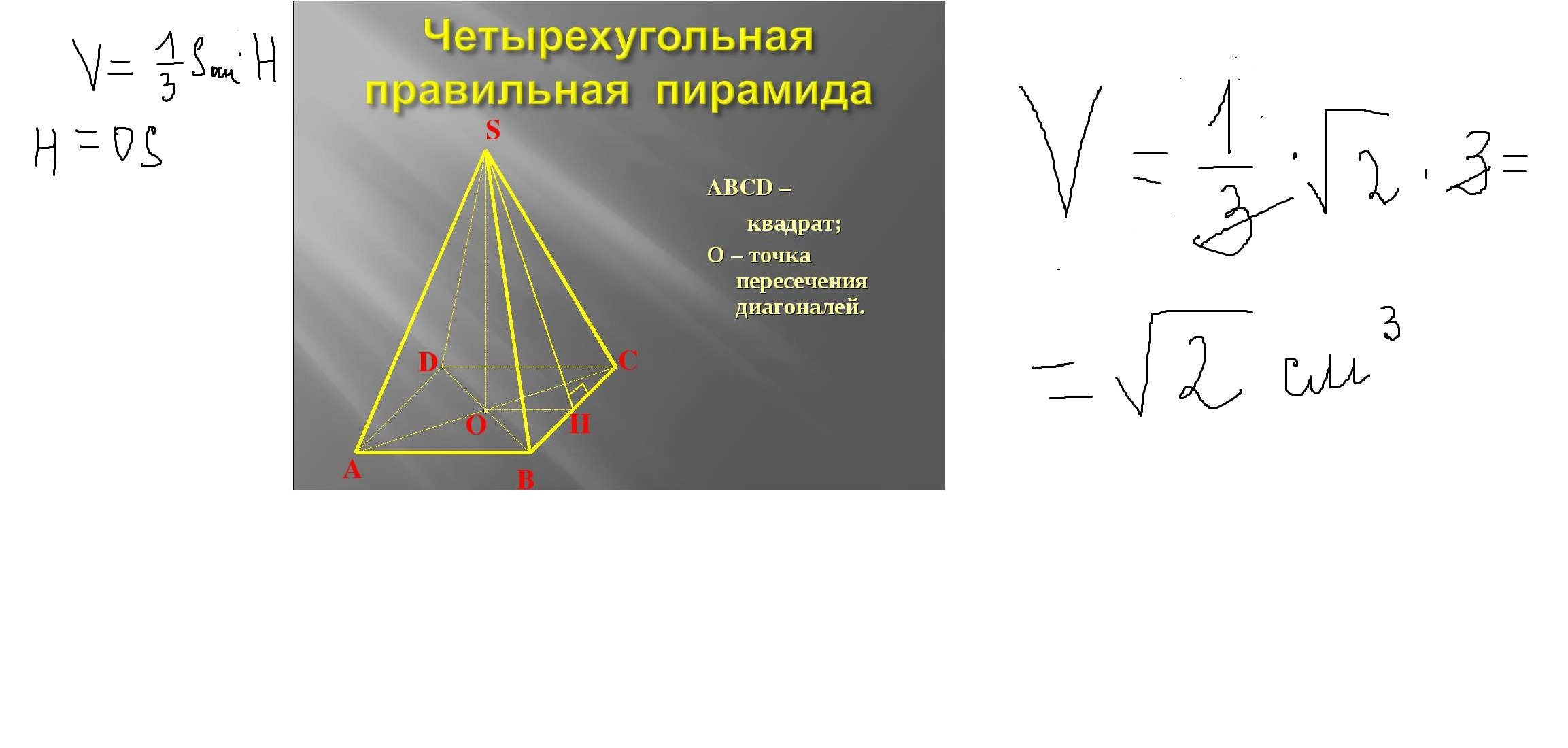
В основании - квадрат.
Диагональ квадрата - d = √2*a = 2√2 - дано.
Сторона квадрата (основания)
a = d /√2 = 2 см - сторона основания.
Рисунок к задаче в приложении.
Объём пирамиды (любой) по формуле: (просто формула объёма)
-объем пирамиды равен одной трети произведения площади основания на высоту.
V = 1/3* S * h, где:
S - площадь основания, h - высота
Вычисляем
S = 2² = 4 см² - площадь основания.
V = 1/3 * 4*3 = 4 см³ - объем - ОТВЕТ