Предмет: Алгебра,
автор: topeleven
Найдите сумму целых решений неравенства
Приложения:
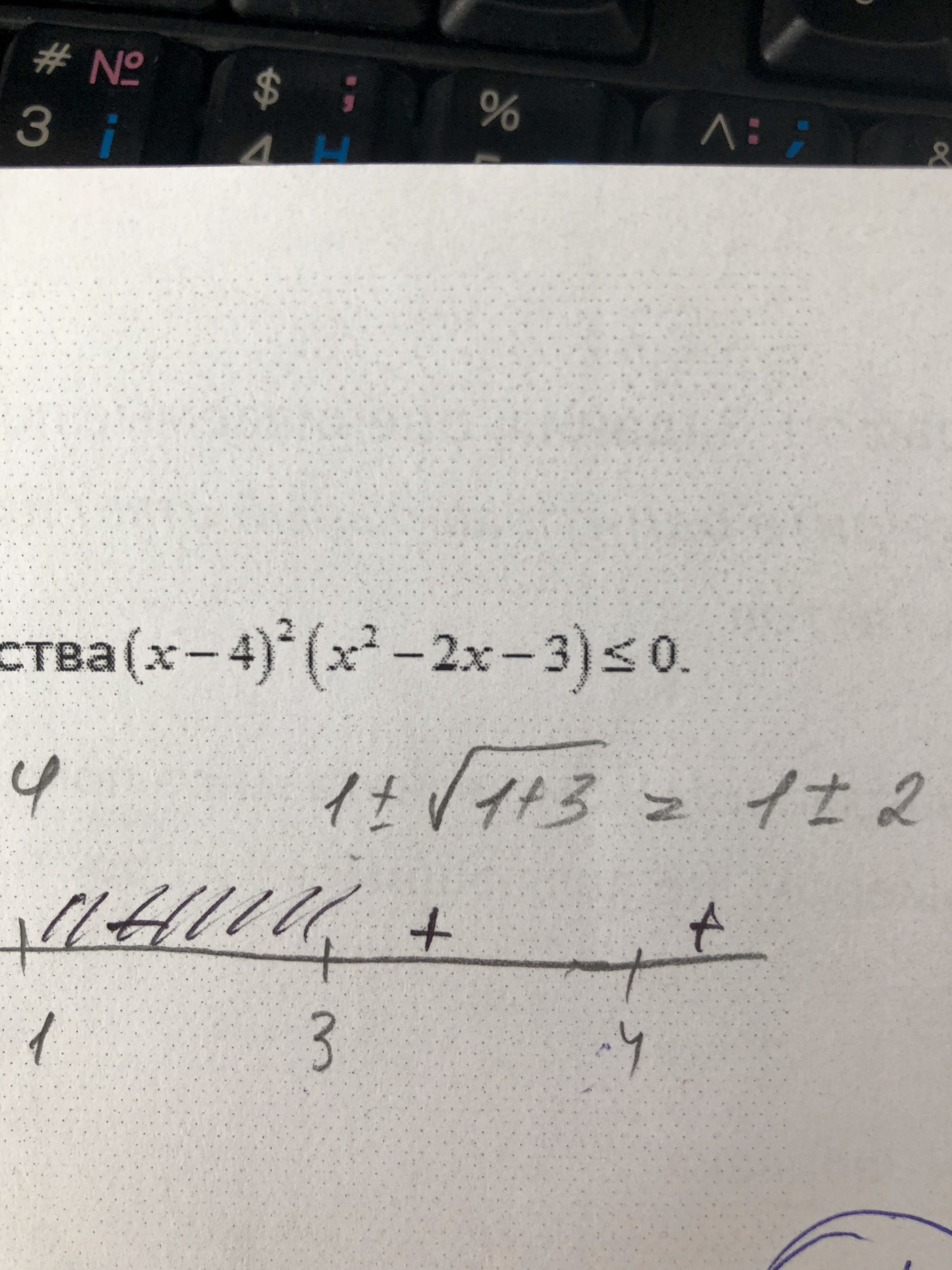
Ответы
Автор ответа:
1
Сумма целых решений = -1+0+1+2+3+4=9
Автор ответа:
0
Решить неравенство
(x – 4)²(x²– 2x – 3) ≤ 0.
Решение я напишу, но объяснение писать не буду, т.к. здесь и так будет все понятно.
{ (x – 4)²≤ 0
{ x²– 2x – 3 ≥ 0
{ (x – 4)²≥ 0
{ x²– 2x – 3 ≤ 0
{ x = 4
{ x∈(– ∞ ; – 1] U [3 ; + ∞)
{ x∈R
{ x∈[– 1 ; 3]
{ x∈[– 1 ; 3] U {4}
Соответственно ответ будет равен:
{ x∈[– 1 ; 3] U {4}
(x – 4)²(x²– 2x – 3) ≤ 0.
Решение я напишу, но объяснение писать не буду, т.к. здесь и так будет все понятно.
{ (x – 4)²≤ 0
{ x²– 2x – 3 ≥ 0
{ (x – 4)²≥ 0
{ x²– 2x – 3 ≤ 0
{ x = 4
{ x∈(– ∞ ; – 1] U [3 ; + ∞)
{ x∈R
{ x∈[– 1 ; 3]
{ x∈[– 1 ; 3] U {4}
Соответственно ответ будет равен:
{ x∈[– 1 ; 3] U {4}
Похожие вопросы
Предмет: Биология,
автор: gunajakberova0
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: olgaralkova
Предмет: Химия,
автор: ZloEDobr9K1337