Question

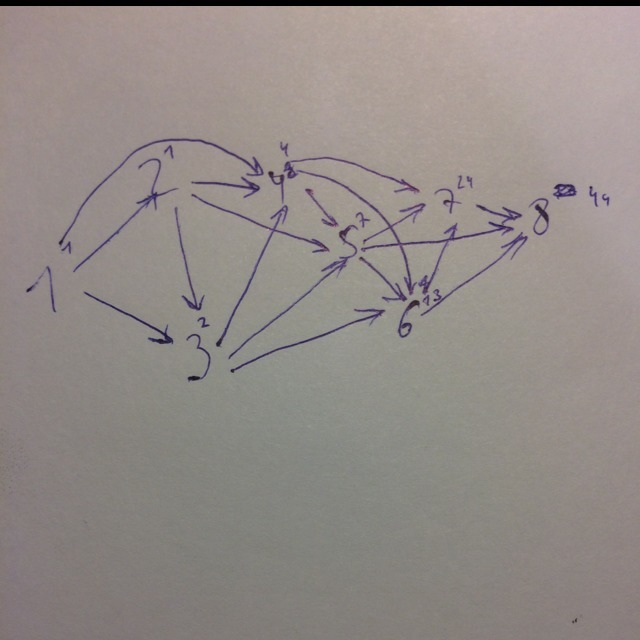
В Тридесятом государстве всего 8 городов, каждые два из которых соединены прямой дорогой. Правитель этого государства решил модернизировать систему автодорог, связывающих города. Он пронумеровал города числами от 1 до 8 в порядке возрастания важности города (самый захолустный город получил номер 1, а столица – номер 8) и ввел одностороннее движение на части дорог, а все остальные дороги закрыл. Одностороннее движение таково: можно проехать от города с номером N до городов с номерами N + 1, N + 2 и N + 3 (если они есть). То есть, работают дороги 1-2, 1-3, 1-4, 2-3, 2-4, 2-5, 3-4, 3-5, 3-6, …, 5-6, 5-7, 5-8, 6-7, 6-8, 7-8.

В обратном направлении по дорогам ехать нельзя, то есть, в частности, в город 1 по новым правилам доехать ни из какого города не получится.

Сколькими способами теперь можно добраться от города с номером 1 до города с номером 8?

Answer 1

Крч,обсчитался 44 путей,в огэ по информатике прям очень стандартная задача есть с путями,так вот тут также складываешь в каждый пункт предыдущее возможное количество путей