Предмет: Математика,
автор: Slakru
Найти область сходимости степенного ряда:
Приложения:
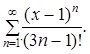
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: ek443540
Предмет: ОБЖ,
автор: agushaaa95
Предмет: Русский язык,
автор: zero9444
Предмет: Математика,
автор: laguna60
Предмет: Алгебра,
автор: aigerim29