Предмет: Математика,
автор: vaniok082
даны векторы a и b которые образуют угол 60 градусов. найти длину вектора c=3а-2b, если длина |a|=3, |b|=4
Ответы
Автор ответа:
9
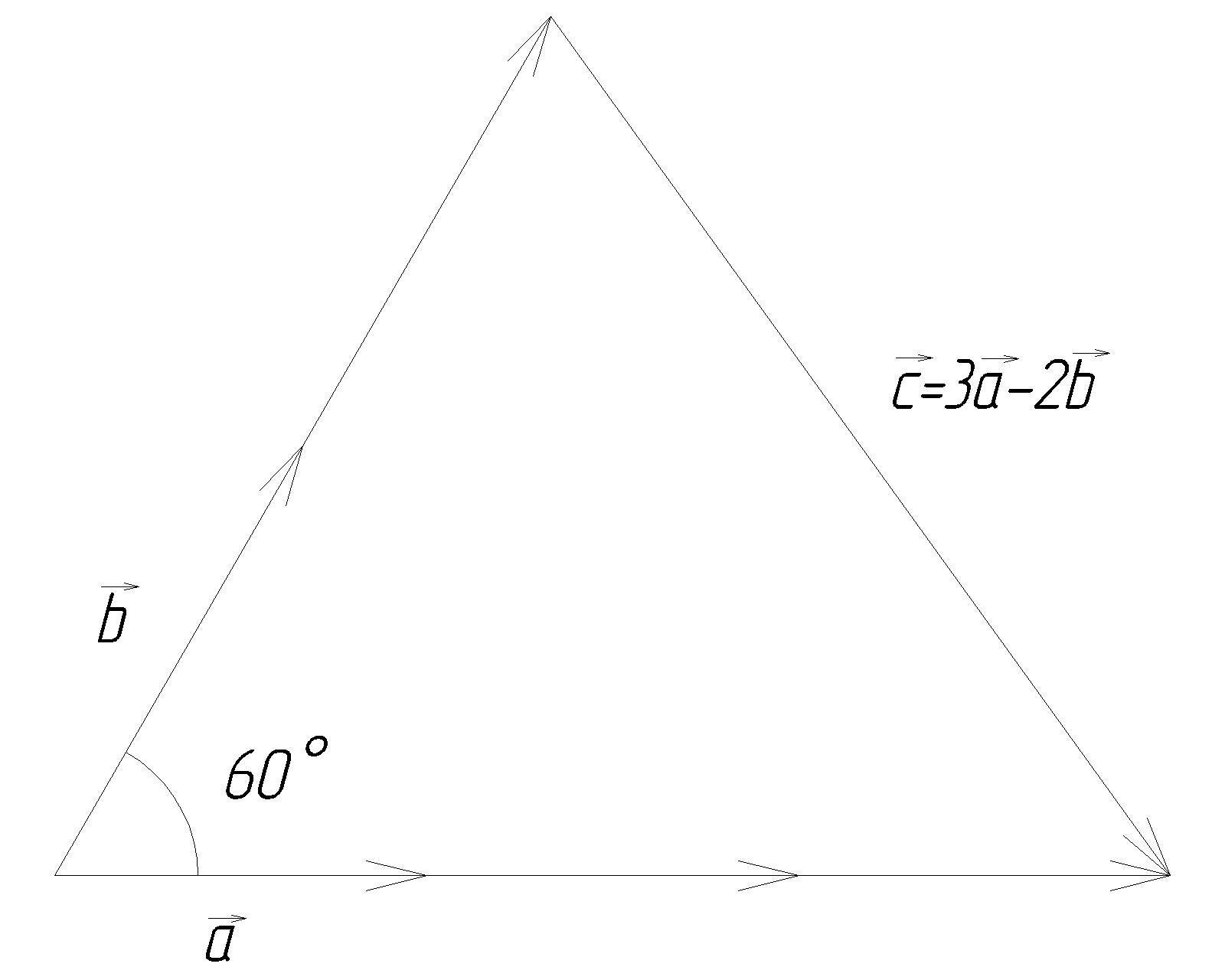
Добавил поясняющий рисунок.
Модуль вектора 3a в 3 раза больше модуля вектора a:

Модуль вектора 2b в 2 раза больше модуля вектора b:

Направление вектора c определяется правилом вычитания векторов. Часто его запоминают так: из какого вектора вычитаем, к его концу и направлен результирующий вектор.
В полученном треугольнике сторону, лежащую напротив угла в 60 градусов (т.е. модуль вектора c), можно найти по теореме косинусов:

Также я добавил рисунок-результат.
Модуль вектора 3a в 3 раза больше модуля вектора a:
Модуль вектора 2b в 2 раза больше модуля вектора b:
Направление вектора c определяется правилом вычитания векторов. Часто его запоминают так: из какого вектора вычитаем, к его концу и направлен результирующий вектор.
В полученном треугольнике сторону, лежащую напротив угла в 60 градусов (т.е. модуль вектора c), можно найти по теореме косинусов:
Также я добавил рисунок-результат.
Приложения:

Похожие вопросы
Предмет: Қазақ тiлi,
автор: didaryasi
Предмет: Литература,
автор: JohnIvanovich
Предмет: Русский язык,
автор: anny7764
Предмет: Алгебра,
автор: ФИЗМАТ11
Предмет: Геометрия,
автор: целя