Предмет: Математика,
автор: samsonik2012
Логарифмические уравнения! Помогите с двумя заданиями
Приложения:
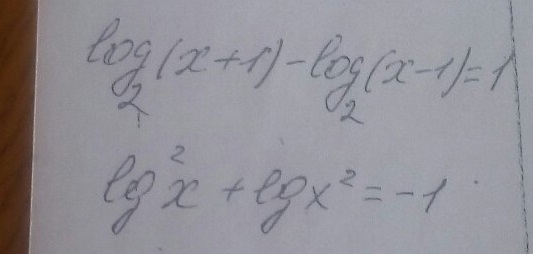
FairHAIR1337:
а второе точно правильно списано?
Ответы
Автор ответа:
2
1)

ОДЗ: х+1>0 и х-1>0; х>-1 и х>1. Следовательно, х>1.
Разность логарифмов равна логарифму частного, т.е.





Дробь равна нулю, если числитель равен нулю, а знаменатель в ноль не обращается:
-х+3=0 и х-1≠0
х=3 и х≠1.
Ответ: х=3.
2)

ОДЗ: х>0
Используя свойство логарифма от степени, уравнение запишем в виде





Ответ : х=1/10.
ОДЗ: х+1>0 и х-1>0; х>-1 и х>1. Следовательно, х>1.
Разность логарифмов равна логарифму частного, т.е.
Дробь равна нулю, если числитель равен нулю, а знаменатель в ноль не обращается:
-х+3=0 и х-1≠0
х=3 и х≠1.
Ответ: х=3.
2)
ОДЗ: х>0
Используя свойство логарифма от степени, уравнение запишем в виде
Ответ : х=1/10.
спасибо. я домой приду - проверю и оценю
Похожие вопросы
Предмет: Английский язык,
автор: katay502
Предмет: Английский язык,
автор: prohornatasa
Предмет: Математика,
автор: milenapermakova
Предмет: Математика,
автор: Аноним