Предмет: Математика,
автор: ezhelinakateri
ВЫЧИСЛИТЬ ЗНАЧЕНИЕ ОБРАТНОЙ ТРИГОНОМЕТРИЧЕСКОЙ ФУНКЦИИ
Приложения:
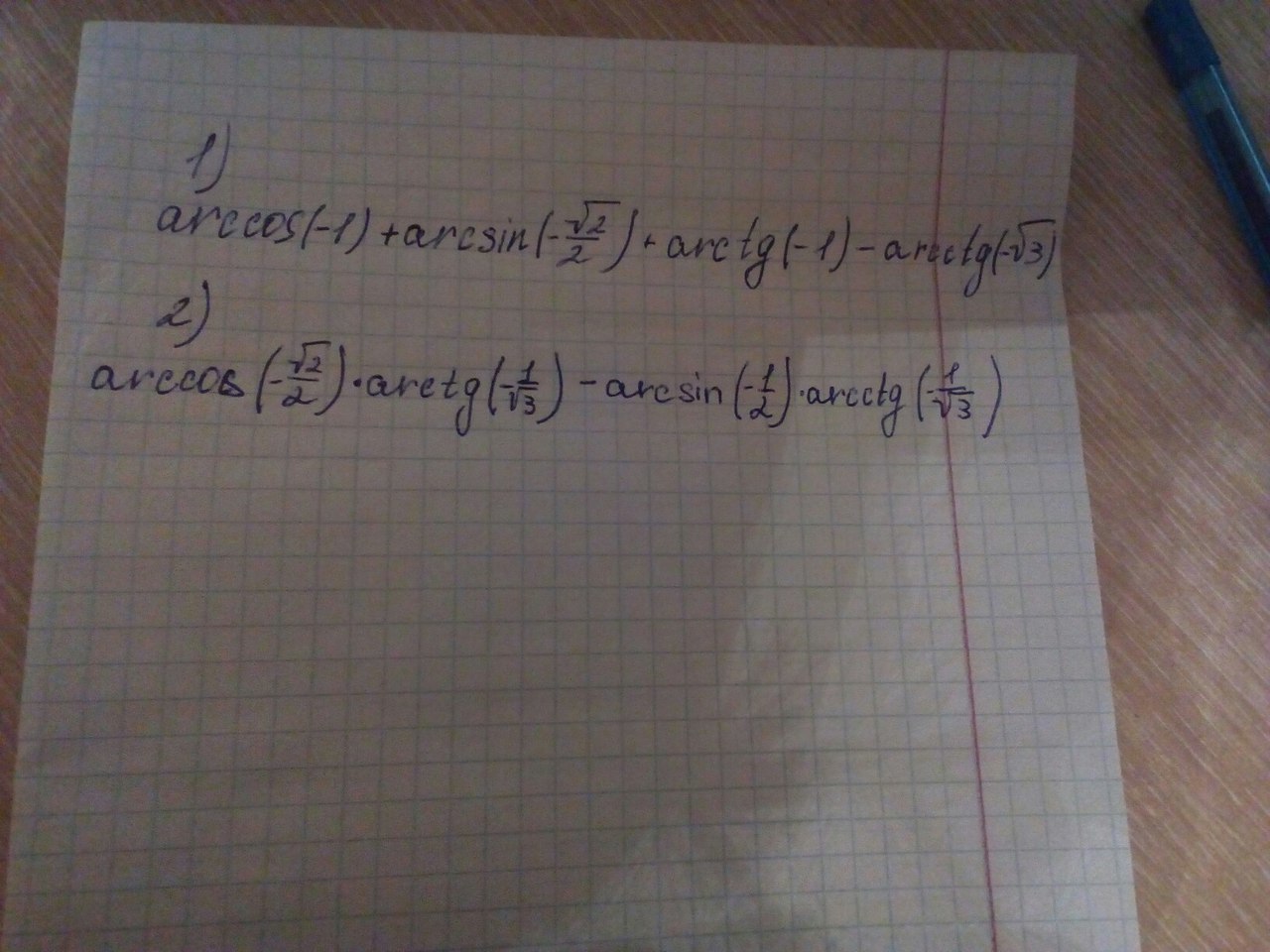
Ответы
Автор ответа:
1
1) 


2)


2)
Похожие вопросы
Предмет: Биология,
автор: 888lina888
Предмет: Физика,
автор: sereginasolomia
Предмет: Немецкий язык,
автор: oper14151175825
Предмет: Биология,
автор: Ninaos
Предмет: Математика,
автор: p16p05