Предмет: Алгебра,
автор: petroretro
Помогите с системой,пожалуйста.Срочно.
Приложения:
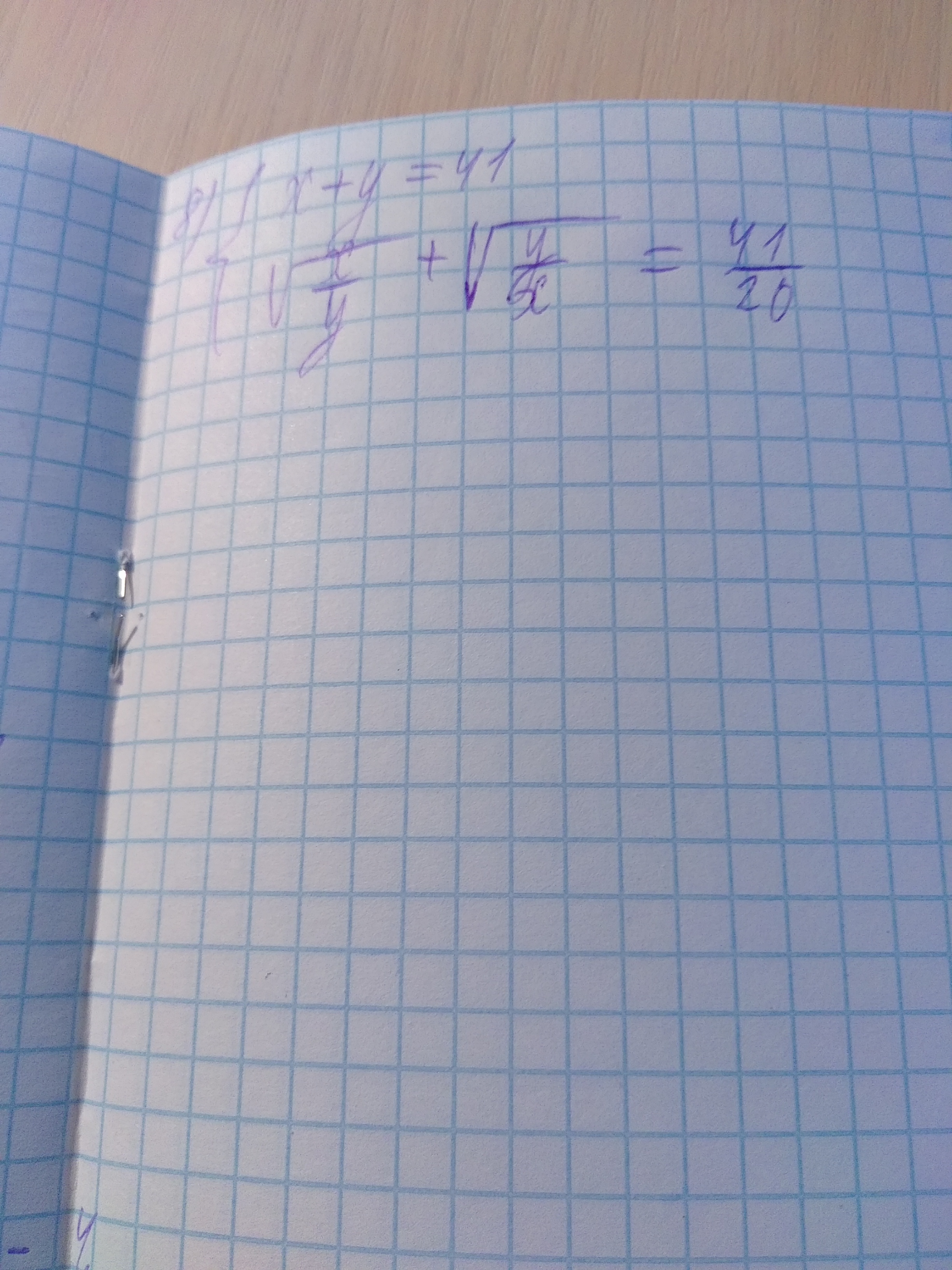
oganesbagoyan:
ОДЗ: x/y >0 , т.е x и y одного знака ,но x+y =41 >0 ⇒ x>0 ,y >0 * * * {x+y =41 ; (x+y)/√xy = 41/20 ⇔ {x+y =41 ; xy = 400 . Виет
Ответы
Автор ответа:
4
Автор ответа:
0
Ффффффффффффффффффффффффффффффффффф
Приложения:
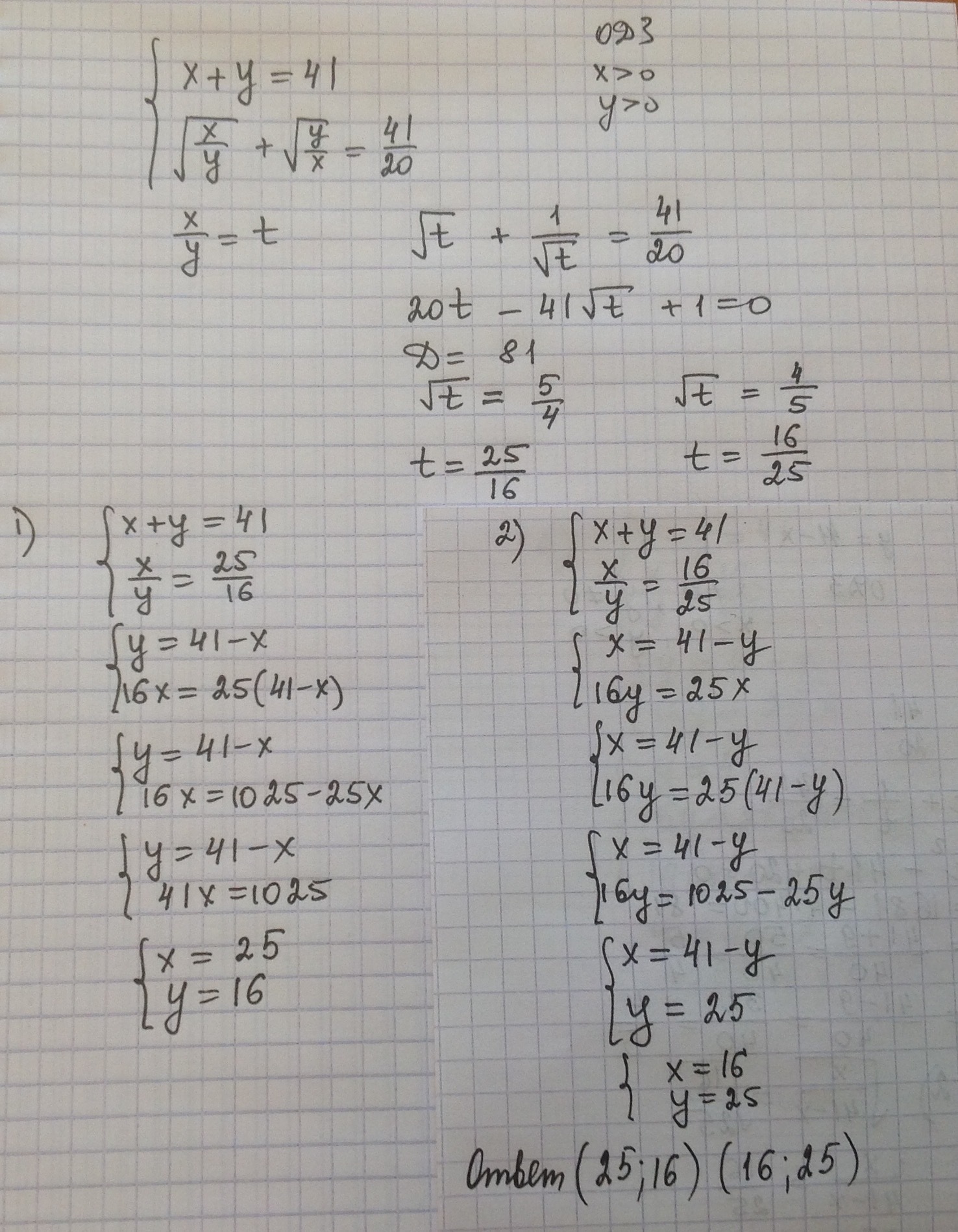
Похожие вопросы
Предмет: Геометрия,
автор: katyagilaykova
Предмет: Алгебра,
автор: bfasyhov
Предмет: Математика,
автор: lala2012lala20
Предмет: Физика,
автор: Rangor1234