Предмет: Алгебра,
автор: foopd
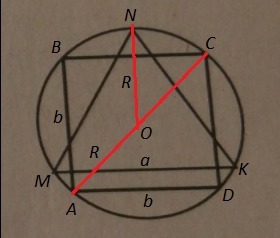
памагите пожалуйста 8 номер
Приложения:

Ответы
Автор ответа:
0
Периметр правильного треугольника = сумме трёх его равных сторон,
то есть .
.

Радиус описанной окружности равен .
.
Но R - радиус описанной окружности равен половине диагонали вписанного квадрата со стороной b, то есть .
.
Диаметр .
.

Периметр квадрата
то есть
Радиус описанной окружности равен
Но R - радиус описанной окружности равен половине диагонали вписанного квадрата со стороной b, то есть
Диаметр
Периметр квадрата
Приложения:
Похожие вопросы
Предмет: Литература,
автор: denisyadiki50
Предмет: Информатика,
автор: kostinaveronika
Предмет: Физика,
автор: hameleonXXX
Предмет: Химия,
автор: Kirill159753