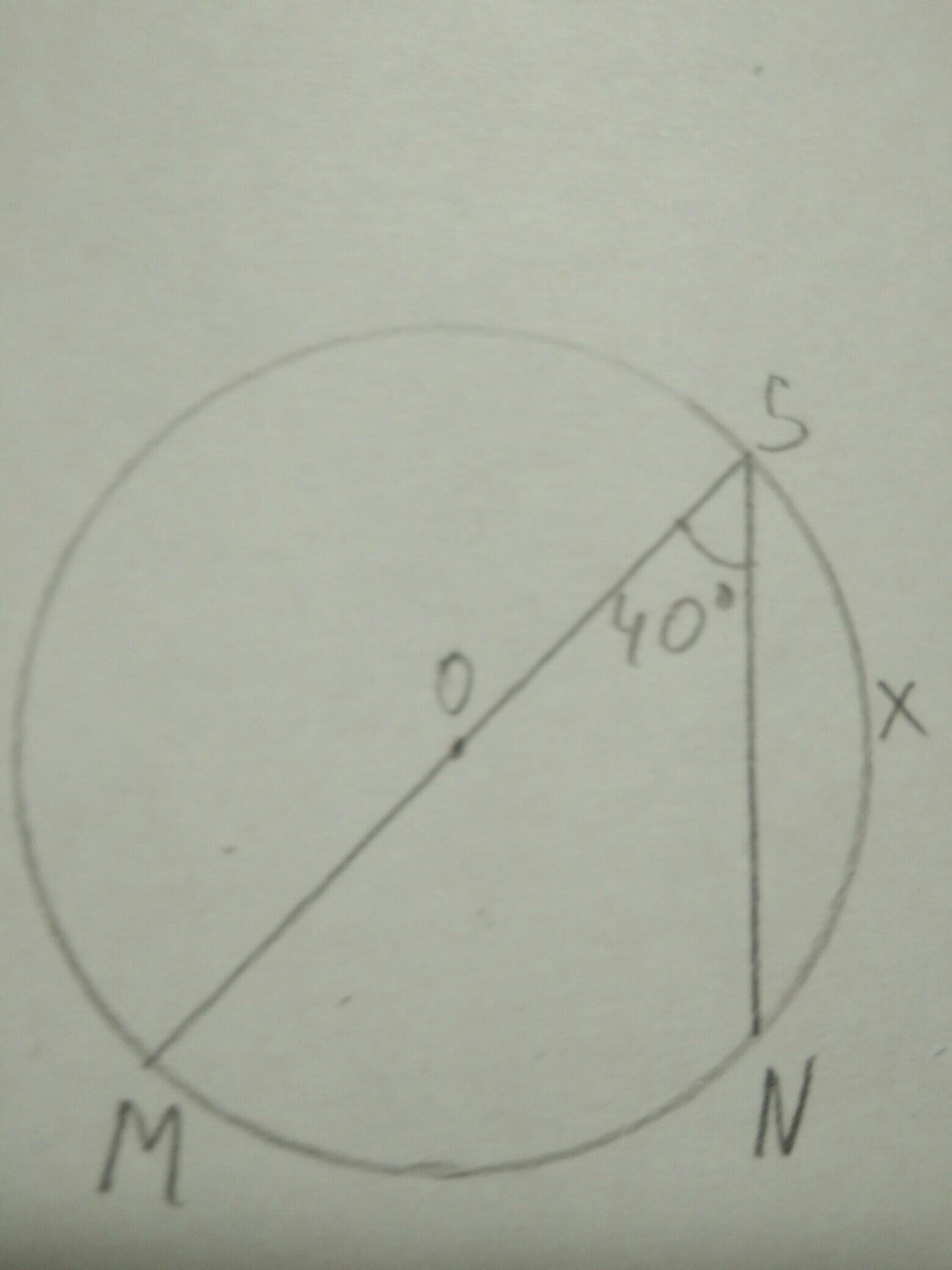
Дано : окружность с центром О угол MSN вписанный равен 40° найти дугу SN
Ответы
Вписанный угол вдвое меньше дуги на которую он опирается. Таким образом ∪MN=2·∠MSN=2·40°=80°.
MS - диаметр, поэтому ∪MS=180°.
∪SN=∪MS-∪MN=180°-80°=100°
Ответ: 100°.

Ответ:
Дуга NS=100°
Объяснение:
Дано:
Окружность с центром в точке О
Вписанный угол ∠MSN = 40°
MS - диаметр
Найти: дугу NS
Решение.
Угол, образованный двумя радиусами называется центральным углом. Так как MS - диаметр, MS = MO + OS, где MO и OS радиусы. Отсюда, ∠MOS - центральный угол и развёрнутый угол, то есть
∠MOS = 180°.
Центральный угол ∠MOS измеряется дугой MS, на которую опирается. Отсюда дуга MS = ∠MOS = 180°.
Вписанный угол ∠MSN измеряется половиной дуги MN, на которую он опирается. Отсюда дуга MN=2·∠MSN=2·40°=80°.
Теперь
дуга NS = дуга MS - дуга MN = 180°-80° = 100°.
Замечание. На рисунке искомая дуга обозначена через х и поэтому соответствует обозначению NS. А дуга SN = дуга SM + дуга MN = 180°+ 80° = 260°.