Предмет: Алгебра,
автор: Fio1232
Найти производную двух этих функций.
Приложения:
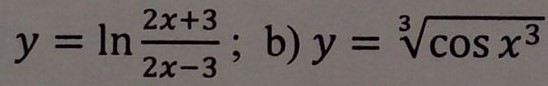
Ответы
Автор ответа:
1
Дмитрий1425:
Вам всё понятно?
Да спасибо огромное
Будут ещё производные пишите ,с большой радостью всё сделаю)
Похожие вопросы
Предмет: История,
автор: lolpinkgoose
Предмет: Информатика,
автор: murtazinsaid2007
Предмет: Астрономия,
автор: Drogan09
Предмет: География,
автор: dahamatka
Предмет: Алгебра,
автор: niccc1