Предмет: Геометрия,
автор: AGZIL
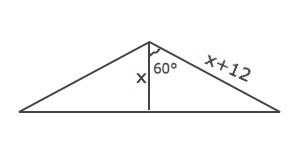
Разность между образующей конуса и его высотой равна 12 , а угол между ними равен 60° . Найти высоту конуса
Ответы
Автор ответа:
3
Т.к. угол между высотой и образующей 60°, угол между образующей и радиусом 30°
Тогда высота - катет прямоугольного треугольника и противолежит углу 30°.
Высота=х,
Гипотенуза ( образующая) = 2х (свойство)
2х-х=12⇒
х=12 ( ед. длины)
---------
Или
Угол между высотой конуса и его образующей 60°.
Высота - катет прямоугольного треугольника, образующая - гипотенуза.
Примем высоту равной х.
Тогда гипотенуза равна (х+12) и равна х:cos60° (cos60°=1/2)
Составим уравнение:
х+12=х:(1/2)⇒
х+12=2х
х=12 (ед. длины)
Тогда высота - катет прямоугольного треугольника и противолежит углу 30°.
Высота=х,
Гипотенуза ( образующая) = 2х (свойство)
2х-х=12⇒
х=12 ( ед. длины)
---------
Или
Угол между высотой конуса и его образующей 60°.
Высота - катет прямоугольного треугольника, образующая - гипотенуза.
Примем высоту равной х.
Тогда гипотенуза равна (х+12) и равна х:cos60° (cos60°=1/2)
Составим уравнение:
х+12=х:(1/2)⇒
х+12=2х
х=12 (ед. длины)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: polinan08
Предмет: Английский язык,
автор: asel2010kaz
Предмет: Математика,
автор: dosherakdomashni
Предмет: Информатика,
автор: k981pe
Предмет: Литература,
автор: владиклай