Question

Запишите уравнение окружности симметричной окружности (x-1)^2+(y+2)^2=1 относительно оси Oy и оси оx

Answer 1

Уравнение окружности имеет вид :

(x - x₀)² + (y - y₀)² = R² ,

где x₀, y₀ - координаты центра окружности, R - радиус окружности

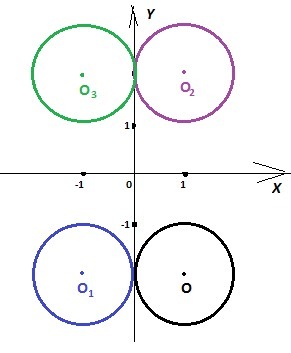
(x - 1)² + (y + 2)² = 1 ⇒ Центр окружности О(1; -2), радиус R=1

При симметрии относительно оси OY радиус и координата у не изменятся, а координата х поменяет знак

(x + 1)² + (y + 2)² = 1 ⇒ Центр окружности O₁(-1; -2), радиус R=1

При симметрии относительно оси OX радиус и координата х не изменятся, а координата у поменяет знак

(x - 1)² + (y - 2)² = 1 ⇒ Центр окружности O₂(1; 2), радиус R=1

При последовательной симметрии относительно осей ОX и OY (центральная симметрия) радиус не изменится, а обе координаты поменяют знаки

(x + 1)² + (y - 2)² = 1 ⇒ Центр окружности O₃(-1; 2), радиус R=1