Предмет: Математика,
автор: НиколайСПБ
Найти неопределенный интеграл
Приложения:
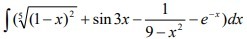
Ответы
Автор ответа:
1
НиколайСПБ:
Я даже и не знаю какой ответ выставить лучшим)
Автор ответа:
3
Похожие вопросы
Предмет: Математика,
автор: nurai240820gmailcom
Предмет: Геометрия,
автор: adilcemilli10
Предмет: Математика,
автор: malboro31
Предмет: Математика,
автор: perepletkina198