Предмет: Математика,
автор: kirill221299
решить уравнение понижением степени
Приложения:
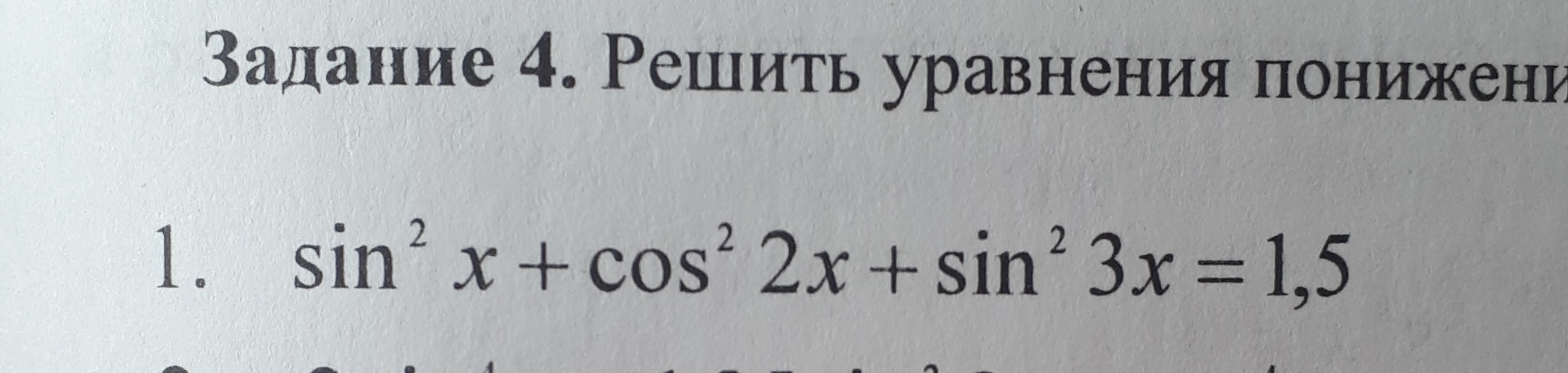
Ответы
Автор ответа:
0
есть формулы: Sin²α = 1/2(1 - Cos2α)
Cos²α = 1/2(1 + Cos2α)
Применим их к нашему уравнению:
1/2(1 - Cos2x) +1/2(1 + Cos4x) +1/2(1 - Cos6x) = 3/2
1 - Cos2x + 1 + Cos4x +1 - Cos6x = 3
- Cos2x + Cos4x - Cos6x = 0
-(Cos2x + Cos6x) + Cos4x = 0
-2Cos4xCos2x + Cos4x = 0
Cos4x(-2Cos2x +1) = 0
Cos4x = 0 или -2Сos2x +1 = 0
4x = π/2 + πk , k∈Z Cos2x = 1/2
x = π/8 + πk/4 , k ∈Z 2x = +-arcCos1/2 + 2πn , n ∈Z
2x = +- π/3 +2πn , n ∈ Z
x = +-π/6 + πn , n∈Z
Cos²α = 1/2(1 + Cos2α)
Применим их к нашему уравнению:
1/2(1 - Cos2x) +1/2(1 + Cos4x) +1/2(1 - Cos6x) = 3/2
1 - Cos2x + 1 + Cos4x +1 - Cos6x = 3
- Cos2x + Cos4x - Cos6x = 0
-(Cos2x + Cos6x) + Cos4x = 0
-2Cos4xCos2x + Cos4x = 0
Cos4x(-2Cos2x +1) = 0
Cos4x = 0 или -2Сos2x +1 = 0
4x = π/2 + πk , k∈Z Cos2x = 1/2
x = π/8 + πk/4 , k ∈Z 2x = +-arcCos1/2 + 2πn , n ∈Z
2x = +- π/3 +2πn , n ∈ Z
x = +-π/6 + πn , n∈Z
Похожие вопросы
Предмет: Математика,
автор: savtyraa
Предмет: Биология,
автор: bershka856
Предмет: Русский язык,
автор: tanirbergenovazhansa
Предмет: Физика,
автор: nike103
Предмет: Алгебра,
автор: evolrp