Предмет: Алгебра,
автор: xFROZx
60 БАЛЛОВ!!! Как решать?
Приложения:
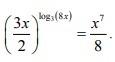
Ответы
Автор ответа:
0
очевидно, первый корень нас не удовлетворяет чисто из-за ОДЗ, поэтому решаем второе под-уравнение и пытаемся найти заведомый икс
найденные корни абсолютно удовлетворяют ОДЗ, поэтому пишем ответ:
tamarabernukho:
x=2
в ответе два корня {2;91.125}
не рассмотрели случай, когда (х/2)=1 , 1 любой степени равно 1
СПАСИБО!
Автор ответа:
1
.............................................................
Приложения:

витиевато однако, можно было просто прологарифмировать по основанию 3. и одз надо написать что x>0. логарифм одзуется
Ну я думаю он бы понял ,что ОДЗ просто x>0
Независимо от того поймет или не поймет, Вы решайте полно со всеми ОДЗ и выкладками. Вы решаете не для него одного, а сейчас для него, а в будущем не один придет и посмотрит решение, а там кто поймет , а кто нет
Я всё понял .Моя вина .В следующий раз учту
Похожие вопросы
Предмет: Математика,
автор: mashket09
Предмет: Немецкий язык,
автор: 1234563434343
Предмет: Английский язык,
автор: nabeiba20080
Предмет: Математика,
автор: zhusan