Предмет: Алгебра,
автор: Hailey7
Решить уравнения (не просто ответ, а с решением)
Приложения:
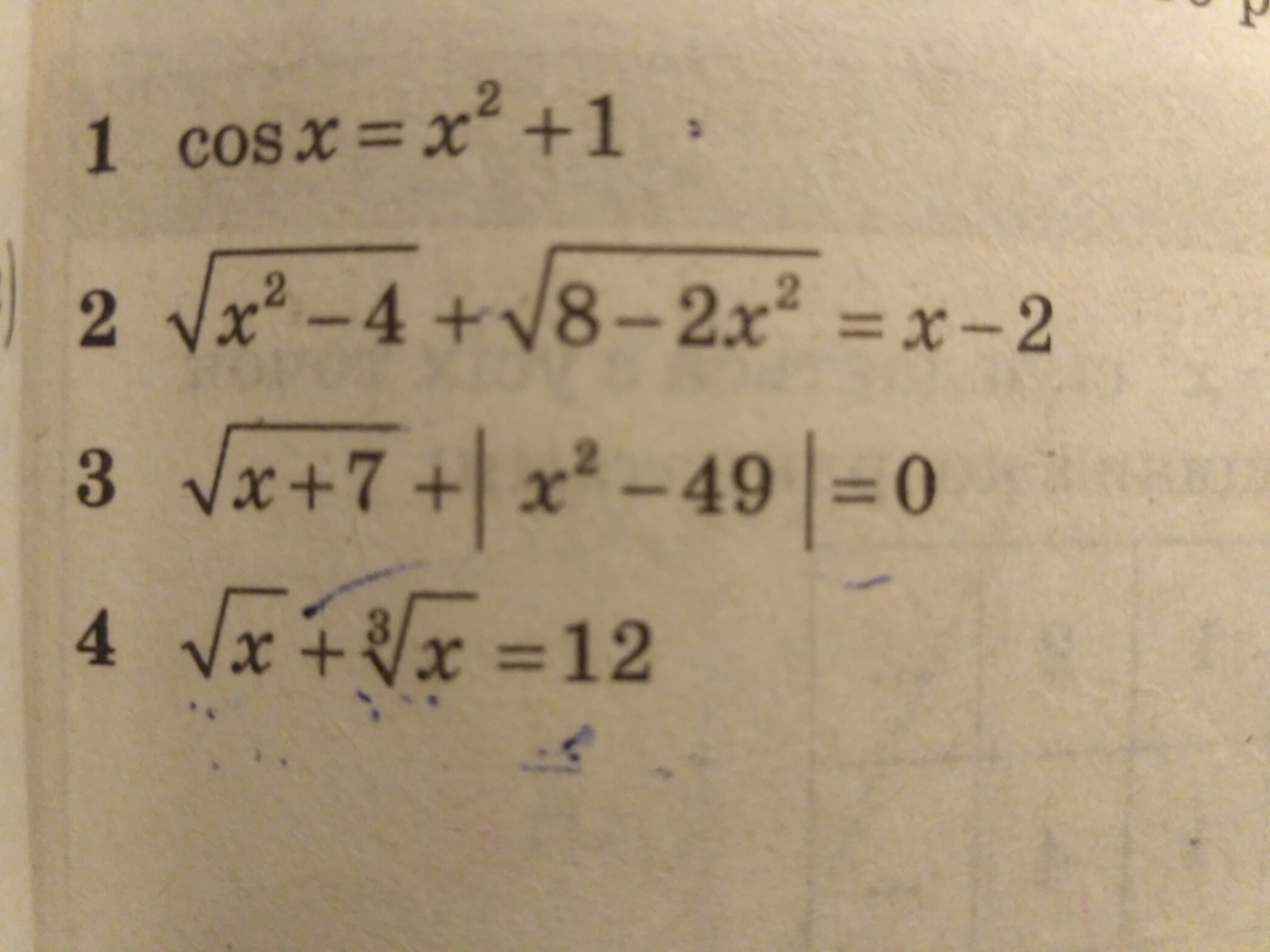
Аноним:
1. Если рассмотреть две функции f(x) = cos x и g(x) = x²+1 то их область значения равны [-1;1] и [1;+∞) соответственно. Графики достигаются лишь в точке (0;1), т.е. х=0 - корень уравнения
Ответы
Автор ответа:
1
1) cos x =x^2 + 1
МЗФ косинуса - [-1; 1]
МЗ выражения справа - [1; ∞)
единственное их равенство при x = 0
cos 0 = 0 + 1
1 = 1
2) √(x^2 - 4) + √(8 - 2x^2) = x - 2
выражение под корнем должно быть неотрицательным
-2 >= x >= 2
-2 <= x <= 2
остаются две точки -2 и 2
сумма двух корней всегда больше или равна 0
Следовательно, нам подходит корень 2
3) модуль и корень всегда больше и равны 0
значит, их сумма больше или равна 0
Тут она равна 0
Следовательно, обе части равны 0
Это происходит в точке x=-7
4) Ставим ОДЗ, что х > 0
Сделаем замену y = x^(1/6)
y^3 + y^2 - 12 = 0
сгруппируем (у меня получилось так)
y^3 + 3y^2 - 2y^2 + 6y - 6y - 12 = 0
y^2(y-2) + 3y(y - 2) + 6(y - 2) = 0
(y-2)(y^2 + 3y + 6) = 0
y = 2
y^2 + 3y + 6 = 0
D = 9 - 24 = -15
D < 0, что значит вещественных корней нет
y = x^(1/6) = 2
x = 2^6 = 64
МЗФ косинуса - [-1; 1]
МЗ выражения справа - [1; ∞)
единственное их равенство при x = 0
cos 0 = 0 + 1
1 = 1
2) √(x^2 - 4) + √(8 - 2x^2) = x - 2
выражение под корнем должно быть неотрицательным
-2 >= x >= 2
-2 <= x <= 2
остаются две точки -2 и 2
сумма двух корней всегда больше или равна 0
Следовательно, нам подходит корень 2
3) модуль и корень всегда больше и равны 0
значит, их сумма больше или равна 0
Тут она равна 0
Следовательно, обе части равны 0
Это происходит в точке x=-7
4) Ставим ОДЗ, что х > 0
Сделаем замену y = x^(1/6)
y^3 + y^2 - 12 = 0
сгруппируем (у меня получилось так)
y^3 + 3y^2 - 2y^2 + 6y - 6y - 12 = 0
y^2(y-2) + 3y(y - 2) + 6(y - 2) = 0
(y-2)(y^2 + 3y + 6) = 0
y = 2
y^2 + 3y + 6 = 0
D = 9 - 24 = -15
D < 0, что значит вещественных корней нет
y = x^(1/6) = 2
x = 2^6 = 64
Похожие вопросы
Предмет: Математика,
автор: anzhelika123t
Предмет: Обществознание,
автор: ellinakasapova10
Предмет: География,
автор: kasenovaaltynai18
Предмет: Математика,
автор: fsdfsdgsdffsdfs
Предмет: Физика,
автор: tombomr