Question

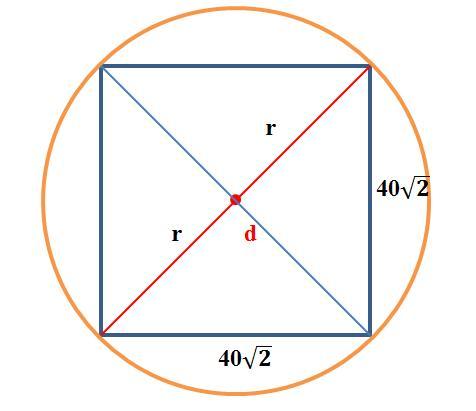
Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата

Answer 1

Ответ:

40 (единиц)

Пошаговое объяснение:

Во-первых, диагональ квадрата делит квадрат на 2 прямоугольные треугольники, во-вторых диагональ квадрата является диаметром окружности описанной около этого квадрата (см. рисунок).

Сторона квадрата a=40$\sqrt{2}$. В силу вышесказанных по теореме Пифагора находим диагональ квадрата, то есть диаметр окружности:

$\displaystyle d^{2} = a^{2} + a^{2} = 2 \cdot a^{2}$

или

$\displaystyle d = \sqrt{2} \cdot a=\sqrt{2} \cdot 40\sqrt{2}=2 \cdot 40=80$ (единиц).

Так как радиус равен половине диаметра, то

r = 80 : 2 = 40 (единиц).