Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, решить. Подробно.
Приложения:
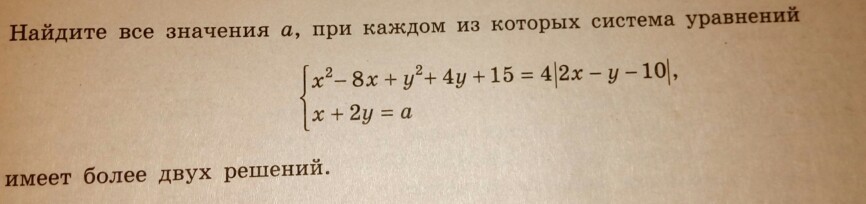
Ответы
Автор ответа:
4
{ x^2-8x+y^2+4y+15=4*|2x-y-10|
{ x+2y=a
Решаем 1 уравнение, оно от а не зависит
1) Если 2x-y-10<0, то
x^2-8x+y^2+4y+15=-8x+4y+40
x^2+y^2+15=40
x^2+y^2=25
Это уравнение окружности с центром О(0;0) и радиусом 5.
При этом 2x-y-10<0, то есть y>2x-10.
Это полуплоскость выше прямой y=2x-10.
Окружность пересекается с прямой в точках (3;-4) и (5;0).
Прямая x+2y=a, то есть y=-x/2+a/2 будет иметь 1 точку пересечения с окружностью при а=-5 (прямая проходит через (3;-4)) и при а=5 (прямая проходит через (5;0), а также
x^2+(-x/2+a/2)^2=25
x^2+x^2/4-ax/2+a^2/4-25=0
4x^2+x^2-2ax+a^2-100=0
5x^2-2ax+a^2-100=0
Найдём точки касания, в которых это уравнение имеет 1 корень.
D/4=a^2-5(a^2-100)=500-4a^2=0
125-a^2=0; a1=-5√5; a2=5√5
Таким образом, при
a € (-5√5;-5] U [5;5√5)
Система имеет 2 корня при условии 2x-y-10<0.
2) Если 2x-y-10>=0, то есть y<=2x-10, то
x^2-8x+y^2+4y+15=8x-4y-40
x^2-16x+y^2+8y=-55
x^2-16x+64-64+y^2+8y+16-16=-55
(x-8)^2+(y+4)^2=80-55=25
Это окружность с центром (8;-4) и радиусом 5.
С прямой y=2x-10 она пересекается в тех же точках (3;-4) и (5;0).
С прямыми y=-x/2+a/2 окружность имеет 1 точку пересечения тоже при а=-5 и а=5, а также
(x-8)^2+(-x/2+a/2+4)^2=25
x^2-16x+64+x^2/4+a^2/4-ax/2-4x+4a+16-25=0
4x^2-64x+x^2+a^2-2ax-16x+16a+220=0
5x^2-80x-2ax+a^2+16a+220=0
D/4=(40+a)^2-5(a^2+16a+220)=0
1600+80a+a^2-5a^2-80a-1100=0
500-4a^2=0
125-a^2=0; a1=-5√5; a2=5√5
Пределы получились точно такие же.
a € (-5√5;-5] U [5;5√5)
Это и есть ответ.
{ x+2y=a
Решаем 1 уравнение, оно от а не зависит
1) Если 2x-y-10<0, то
x^2-8x+y^2+4y+15=-8x+4y+40
x^2+y^2+15=40
x^2+y^2=25
Это уравнение окружности с центром О(0;0) и радиусом 5.
При этом 2x-y-10<0, то есть y>2x-10.
Это полуплоскость выше прямой y=2x-10.
Окружность пересекается с прямой в точках (3;-4) и (5;0).
Прямая x+2y=a, то есть y=-x/2+a/2 будет иметь 1 точку пересечения с окружностью при а=-5 (прямая проходит через (3;-4)) и при а=5 (прямая проходит через (5;0), а также
x^2+(-x/2+a/2)^2=25
x^2+x^2/4-ax/2+a^2/4-25=0
4x^2+x^2-2ax+a^2-100=0
5x^2-2ax+a^2-100=0
Найдём точки касания, в которых это уравнение имеет 1 корень.
D/4=a^2-5(a^2-100)=500-4a^2=0
125-a^2=0; a1=-5√5; a2=5√5
Таким образом, при
a € (-5√5;-5] U [5;5√5)
Система имеет 2 корня при условии 2x-y-10<0.
2) Если 2x-y-10>=0, то есть y<=2x-10, то
x^2-8x+y^2+4y+15=8x-4y-40
x^2-16x+y^2+8y=-55
x^2-16x+64-64+y^2+8y+16-16=-55
(x-8)^2+(y+4)^2=80-55=25
Это окружность с центром (8;-4) и радиусом 5.
С прямой y=2x-10 она пересекается в тех же точках (3;-4) и (5;0).
С прямыми y=-x/2+a/2 окружность имеет 1 точку пересечения тоже при а=-5 и а=5, а также
(x-8)^2+(-x/2+a/2+4)^2=25
x^2-16x+64+x^2/4+a^2/4-ax/2-4x+4a+16-25=0
4x^2-64x+x^2+a^2-2ax-16x+16a+220=0
5x^2-80x-2ax+a^2+16a+220=0
D/4=(40+a)^2-5(a^2+16a+220)=0
1600+80a+a^2-5a^2-80a-1100=0
500-4a^2=0
125-a^2=0; a1=-5√5; a2=5√5
Пределы получились точно такие же.
a € (-5√5;-5] U [5;5√5)
Это и есть ответ.
Кариночка78:
Спасибо огромное)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: Аноним
Предмет: Литература,
автор: rinatylianuar
Предмет: Алгебра,
автор: ladka12
Предмет: Математика,
автор: ivannikovb