Предмет: Алгебра,
автор: catmartovski
Срочно нужна помощь зайчики помогите 40 баллов
Приложения:

Ответы
Автор ответа:
1
вроде как-то так......
Приложения:
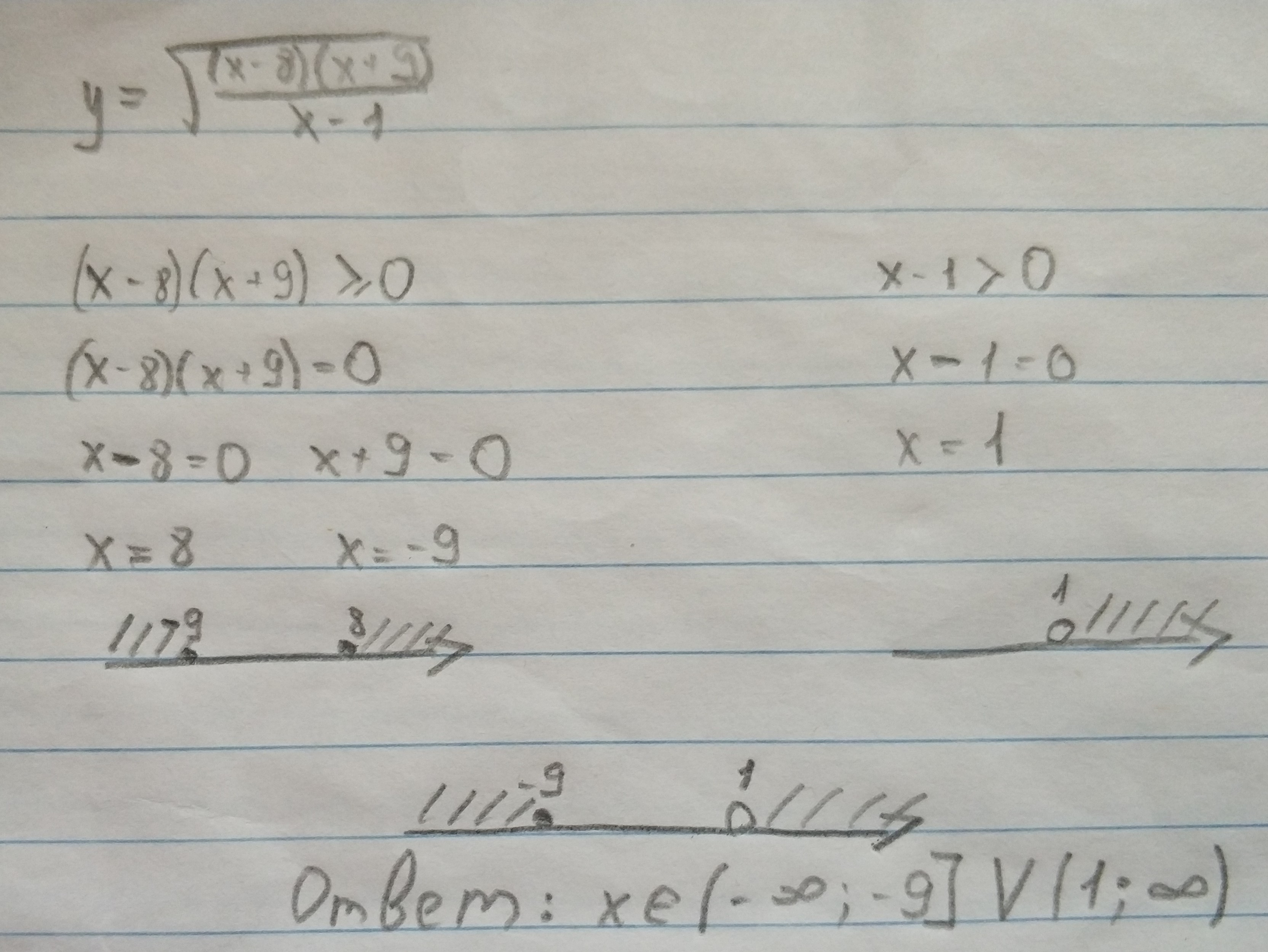
Автор ответа:
2
Подкоренное выражение неотрицательно, т.е.


Найдём корни:
х-8 = 0 => x₁ = 8
x+9 = 0 => x₂ = - 9
x-1 ≠ 0 => x₃ ≠ 1
Откладываем на числовой прямой эти точки.
_________|______________|______________|_______________
-9 1 8
Получили четыре промежутка:
[-∞; -9] ; [-9; 1[ ; ]1; 8] ; [8; +∞[
Определим знак на каждом из этих промежутков.
1) [-∞; -9]
Подставим вместо х любое число из этого промежутка.
при х = 10
(-10-8)(-10+9)/(-10-1) = (-18)(-1)/(-11) = - 18/11 < 0 (знак "-")
2) [-9; 1[
при х=0
(0-8)(0+9)/(0-1) = (-8)·9/(-1) = - 72/(-1) = 72 > 0 (знак "+")
3) ]1; 8]
при х = 5
(5-8)(5+9)/(5-1) = (-3)·14/4 = - 42/4 < 0 (знак "-")
4) [8; +∞[
при х=10
(10-8)(10+9)/(10-1) = 2·18/9 = 4 > 0 (знак "+")
Подходят второй и четвертый промежутки.
Ответ: х ∈ [-9; 1[∪[8; +∞[
Найдём корни:
х-8 = 0 => x₁ = 8
x+9 = 0 => x₂ = - 9
x-1 ≠ 0 => x₃ ≠ 1
Откладываем на числовой прямой эти точки.
_________|______________|______________|_______________
-9 1 8
Получили четыре промежутка:
[-∞; -9] ; [-9; 1[ ; ]1; 8] ; [8; +∞[
Определим знак на каждом из этих промежутков.
1) [-∞; -9]
Подставим вместо х любое число из этого промежутка.
при х = 10
(-10-8)(-10+9)/(-10-1) = (-18)(-1)/(-11) = - 18/11 < 0 (знак "-")
2) [-9; 1[
при х=0
(0-8)(0+9)/(0-1) = (-8)·9/(-1) = - 72/(-1) = 72 > 0 (знак "+")
3) ]1; 8]
при х = 5
(5-8)(5+9)/(5-1) = (-3)·14/4 = - 42/4 < 0 (знак "-")
4) [8; +∞[
при х=10
(10-8)(10+9)/(10-1) = 2·18/9 = 4 > 0 (знак "+")
Подходят второй и четвертый промежутки.
Ответ: х ∈ [-9; 1[∪[8; +∞[
catmartovski:
большое человеческое спасибо <3
Похожие вопросы
Предмет: Алгебра,
автор: sashaivanovarr
Предмет: Другие предметы,
автор: anfisa7291
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: вероника391
Предмет: Математика,
автор: BaxVac