Предмет: Алгебра,
автор: mariamsolod
Пожалуйста, решите неравенство!
Приложения:
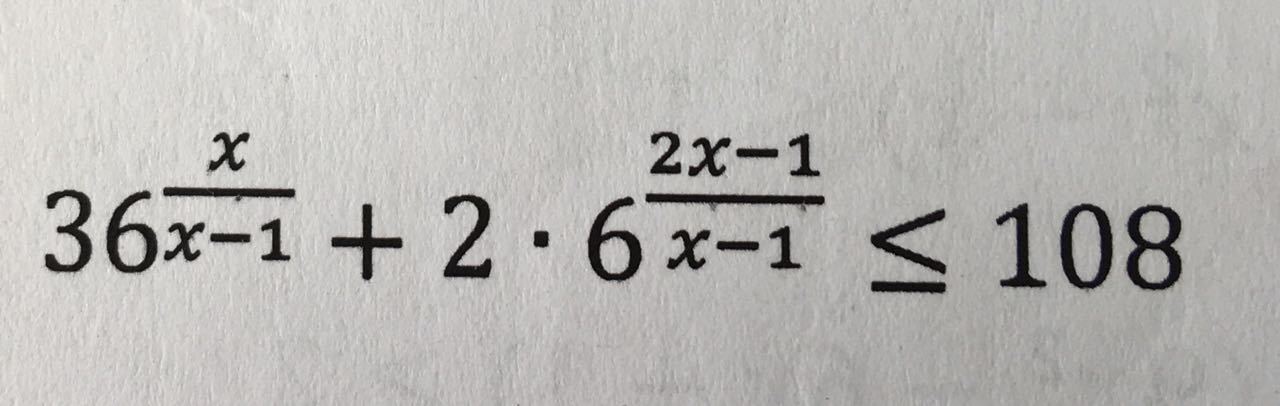
Ответы
Автор ответа:
0
разделим на 36
Автор ответа:
1
task/28448691
-------------------
x /(x-1)= (x-1+1) /(x-1) = 1 +1/(x-1) ;
(2x - 1)/(x-1) = (2x - 2 +1) / (x-1) = 2 + 1 /(x-1) ;
-------------------
x /(x-1)= (x-1+1) /(x-1) = 1 +1/(x-1) ;
(2x - 1)/(x-1) = (2x - 2 +1) / (x-1) = 2 + 1 /(x-1) ;
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: sofia8971
Предмет: Математика,
автор: azincenko898
Предмет: История,
автор: kajyrkenovaalbina
Предмет: Математика,
автор: 89689894227
Предмет: Алгебра,
автор: dashulyakotova