Предмет: Математика,
автор: Devitry
Решить неравенство:
log1/2 (2x-4)≥log1/2 (1+x)
Ответы
Автор ответа:
5
Область допустимых значений:
2x - 4 > 0
1 + x > 0
2x > 4
x > - 1
x > 2
x > -1
Т.о ОДЗ: х > 2
Решаем неравенство:
Так как основание 1/2 < 1, то меняем знак неравенства на противоположный




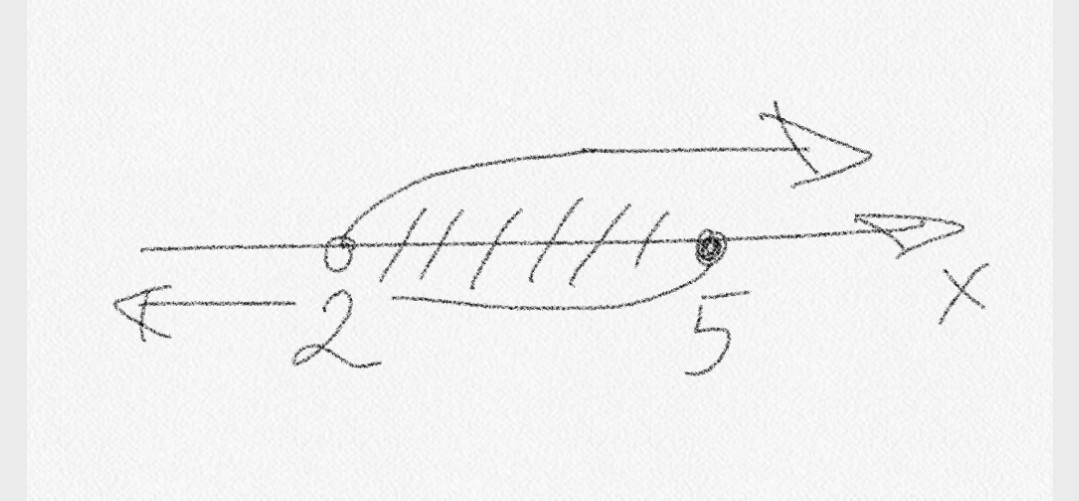
Пересекаем ОДЗ с решением неравенства (фото):
Получаем что X принадлежит (2;5]
2x - 4 > 0
1 + x > 0
2x > 4
x > - 1
x > 2
x > -1
Т.о ОДЗ: х > 2
Решаем неравенство:
Так как основание 1/2 < 1, то меняем знак неравенства на противоположный
Пересекаем ОДЗ с решением неравенства (фото):
Получаем что X принадлежит (2;5]
Приложения:
Похожие вопросы
Предмет: Математика,
автор: omiss6906
Предмет: Русский язык,
автор: anyakagitina10
Предмет: Геометрия,
автор: arisakoreppnova
Предмет: Математика,
автор: 005522qq
Предмет: Математика,
автор: ruslana0506