Предмет: Математика,
автор: HYFR
Найти неопределенные интегралы
Приложения:
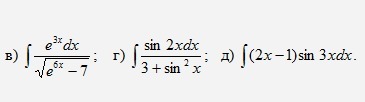
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: muratovaalisha
Предмет: Математика,
автор: alenacapkova780
Предмет: Математика,
автор: htanirberdi
Предмет: История,
автор: Вероника21111
Предмет: Математика,
автор: viphoneybelch