Предмет: Математика,
автор: дадзи
ребят помогите ,не получается решить...
Приложения:
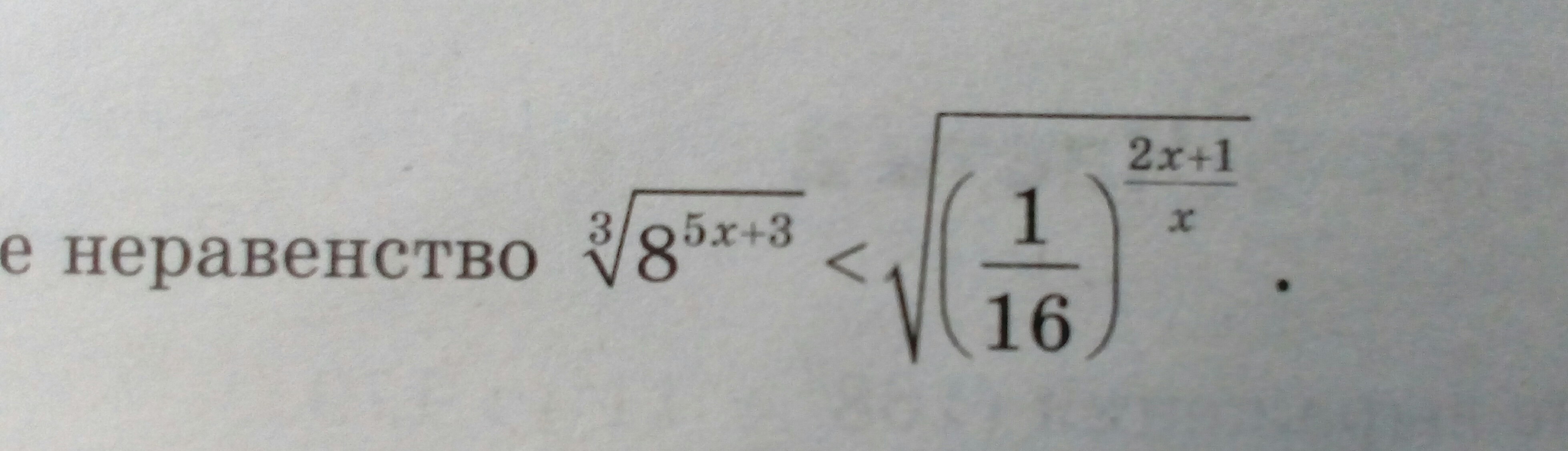
Ответы
Автор ответа:
4
2^5x+3<2^-2(2x+1)/x
2^5x+3<2^-4x+2/x
5x+3<-4x+2/x
5x+3+/4x+2/x<0
5x^2+3x+4x+2/x<0
5x^2+7x+2/x<0
xЭ(перевернутая) (-бесконечность,-1) U(-2/5, 0)
2^5x+3<2^-4x+2/x
5x+3<-4x+2/x
5x+3+/4x+2/x<0
5x^2+3x+4x+2/x<0
5x^2+7x+2/x<0
xЭ(перевернутая) (-бесконечность,-1) U(-2/5, 0)
Rabant:
У тебя знак меньше . Это значит нужный промежуток между , значит x(-1;-2/5)
Автор ответа:
1
и как это понять?
F5
ну
четко
откуда вы взяли 5x3?
5x+3?
степень
аа,поняла, просто у вас в примере написано 5x3
там такого нет
ну вот теперь всё норм
Похожие вопросы
Предмет: История,
автор: ayaumillkyway
Предмет: Химия,
автор: karambaba641
Предмет: Математика,
автор: katasotinova
Предмет: Математика,
автор: ViktoriyaPlay1999
Предмет: Литература,
автор: belca90