Предмет: Геометрия,
автор: Аноним
Помогите срочноооо!!!! Даю 10 баллов!!! Номер 7,8,9
Приложения:

Ответы
Автор ответа:
2
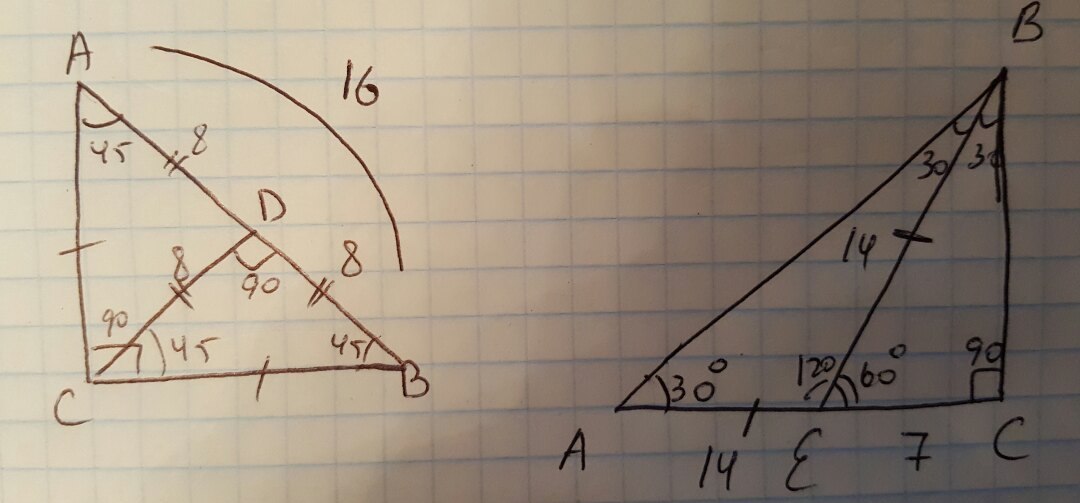
7.
Дано:
ABC - прямоугольный треугольник.
∠ABC = 45.
∠ACB = 90.
∠CDB = 90.
CD = 8.
Найти: AB.
Решение.
Рассмотрим треугольник ABC.
Зная ∠ACB (90) и ∠ABC (45), найдем ∠BAC:
∠BAC = 180 - (90 + 45) = 180 - 135 = 45.
∠BAC = ∠ABC = 45.
Из этого следует, что AC = CB, т.к. углы при основании равны и треугольник ABC - равнобедренный. По свойству прямоугольного треугольника, CD делит прямой угол ACB пополам:
∠DCB = 90/2 = 45.
∠DCB = ∠DBC = ∠DCA = 45.
Исходя из этого, ∠DAC = ∠DCA = 45, они являются углами при основании треугольника DCA. Из этого следует, что AD = DC = 8.
Рассмотрим треугольник DCB. Получаем, что ∠DCB = ∠DBC, они являются углами при основании, что значит DC = DB = 8.
Получаем:
AB = AD + DB = 8 + 8 = 16.
Ответ: 16.
8.
Дано:
∠BEC = 60.
∠DCE = 90.
∠BAE = 30.
Найти: AE.
Решение.
Треугольник BEC - прямоугольный, так как ∠DCE = 90.
Найдем ∠CBE = 180 - (90 + 60) = 180 - 150 = 30.
Так как катет лежит напротив угла в 30 градусов, то он является половиной гипотенузы BE.
BE = 2*EC = 14.
Найдем ∠BEA, как смежный:
∠BEA = 180 - 60 = 120.
Найдем ∠BAE.
∠ABE = 180 - (120 + 30) = 180 - 150 = 30.
∠ABE = ∠BAE = 30 ⇒ AE = BE = 14.
Ответ: 14.
Дано:
ABC - прямоугольный треугольник.
∠ABC = 45.
∠ACB = 90.
∠CDB = 90.
CD = 8.
Найти: AB.
Решение.
Рассмотрим треугольник ABC.
Зная ∠ACB (90) и ∠ABC (45), найдем ∠BAC:
∠BAC = 180 - (90 + 45) = 180 - 135 = 45.
∠BAC = ∠ABC = 45.
Из этого следует, что AC = CB, т.к. углы при основании равны и треугольник ABC - равнобедренный. По свойству прямоугольного треугольника, CD делит прямой угол ACB пополам:
∠DCB = 90/2 = 45.
∠DCB = ∠DBC = ∠DCA = 45.
Исходя из этого, ∠DAC = ∠DCA = 45, они являются углами при основании треугольника DCA. Из этого следует, что AD = DC = 8.
Рассмотрим треугольник DCB. Получаем, что ∠DCB = ∠DBC, они являются углами при основании, что значит DC = DB = 8.
Получаем:
AB = AD + DB = 8 + 8 = 16.
Ответ: 16.
8.
Дано:
∠BEC = 60.
∠DCE = 90.
∠BAE = 30.
Найти: AE.
Решение.
Треугольник BEC - прямоугольный, так как ∠DCE = 90.
Найдем ∠CBE = 180 - (90 + 60) = 180 - 150 = 30.
Так как катет лежит напротив угла в 30 градусов, то он является половиной гипотенузы BE.
BE = 2*EC = 14.
Найдем ∠BEA, как смежный:
∠BEA = 180 - 60 = 120.
Найдем ∠BAE.
∠ABE = 180 - (120 + 30) = 180 - 150 = 30.
∠ABE = ∠BAE = 30 ⇒ AE = BE = 14.
Ответ: 14.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Литература,
автор: Foqul
Предмет: Литература,
автор: Аноним
Предмет: Биология,
автор: 1Ева1
Предмет: Математика,
автор: ага4