Предмет: Алгебра,
автор: pochinov228
Помогите пожалуйста!!!
Номер 87,88
Приложения:
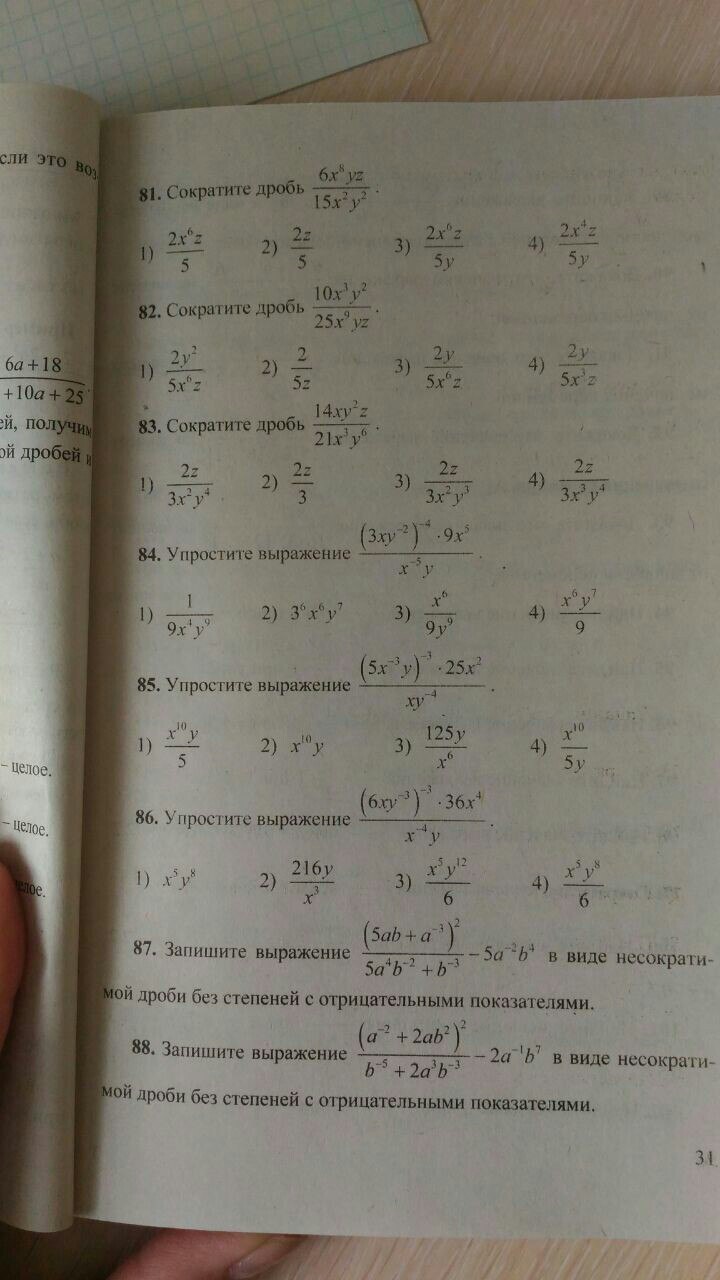
arinab01p0c2kd:
??
Ответы
Автор ответа:
1
Автор ответа:
0
Возможно где то со степенями косяк в 88 , рекомендую перепроверить на всякий
Похожие вопросы
Предмет: Астрономия,
автор: Аноним
Предмет: Математика,
автор: rustambekmurod60
Предмет: Английский язык,
автор: ZITAa
Предмет: Биология,
автор: farmansukeymanov
Предмет: Биология,
автор: Арюна123456789