Question

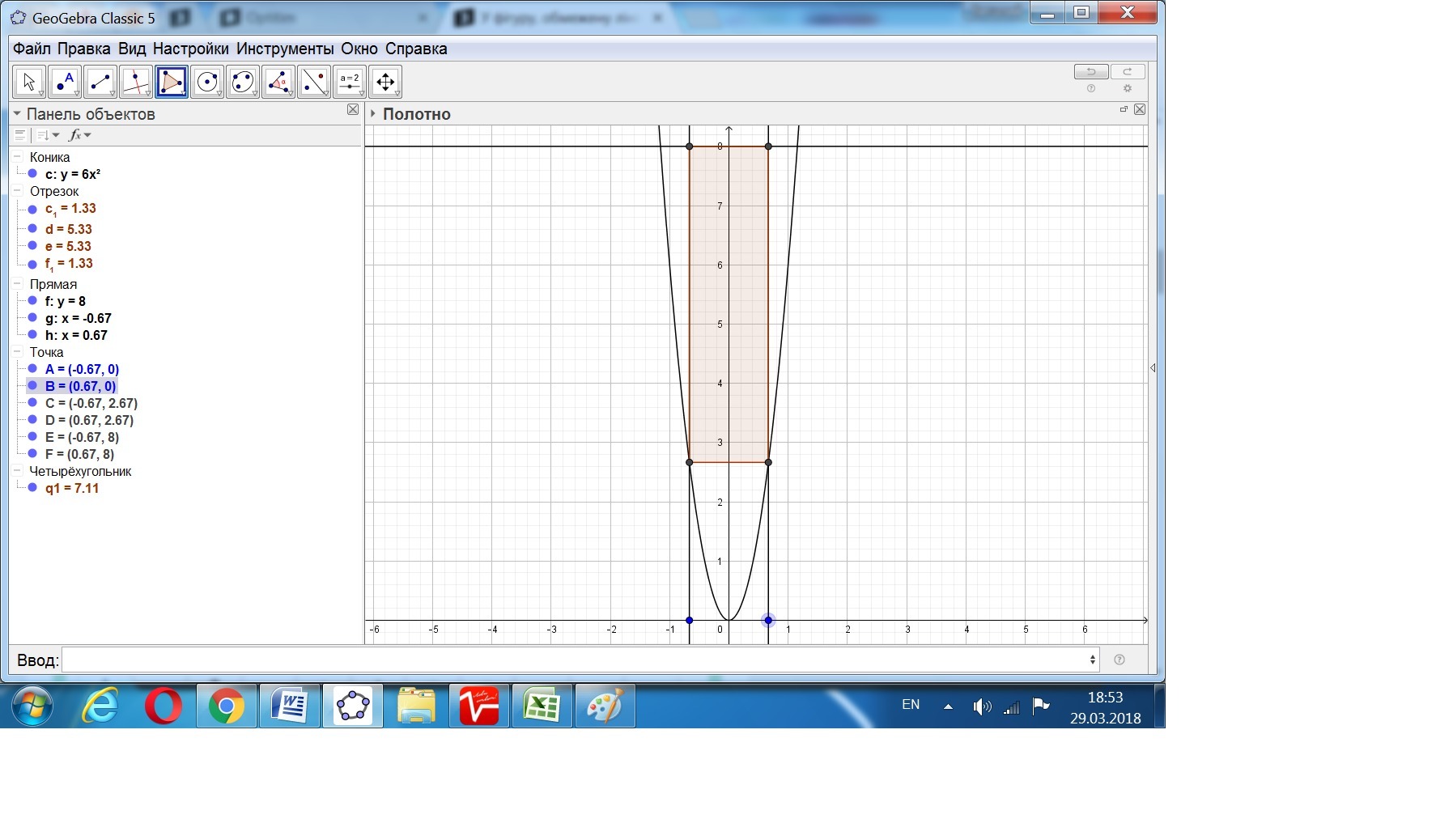
У фігуру, обмежену лініями y=6x^2 та y=8вписано прямокутник найбільшої площі., так що 2 його вешини лежать на прямій, а дві інші- на параболі. Знайдіть координати вершин цього прямокутника та його площу

Answer 1

Примем на параболе точку с абсциссой х и ординатой 6х².
Тогда площадь S заданного прямоугольника будет равна:
S = 2x*(8 - 6x²) = 16x - 12x³.
Найдём максимум найденной функции, приравняв производную нулю.
S' = 16 - 36x².
16 - 36x² = 0,
x² = 16/36.
x = √(16/36) = +-(4/6) = +-(2/3). у = 6*(4/9) = 8/3.
Координаты вершин: ((-2/3); (8/3), ((-2/3); 8), ((2/3); (8/3) и ((2/3); (8).
Подставим значение х = (2/3) в уравнение площади:
S = 16*(2/3) - 12*(2/3)³ = (32/3) - (96/27) = 192/27 = 64/9 ≈ 7,1111 кв.ед.