Question

ПОМОГИТЕ ПОЖАЛУЙСТА ЗАВТРА КОНТРОЛЬНАЯ

Answer 1

№57.
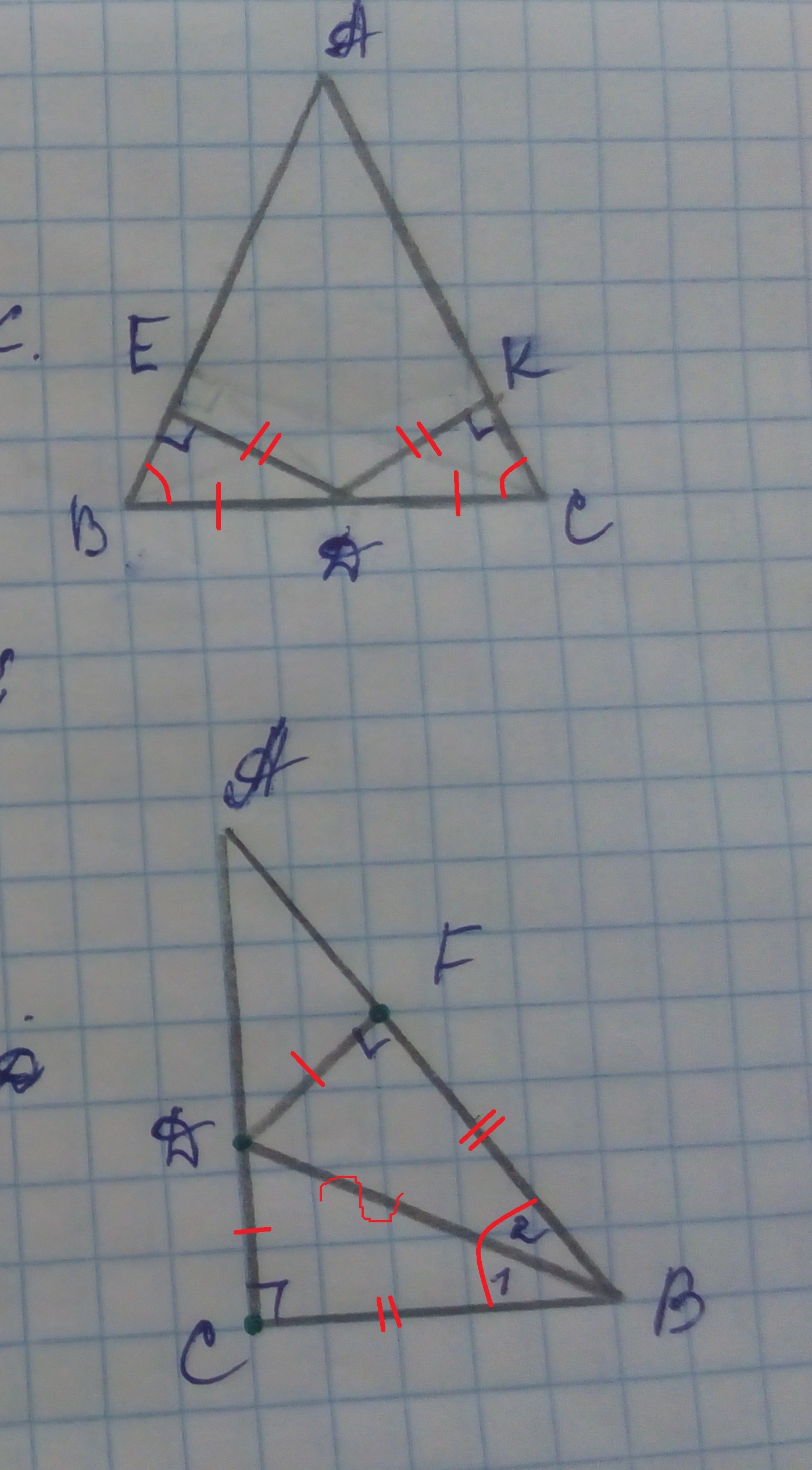
ДАНО : ΔАВС 
т.D - середина ВС
DE⊥АВ
ВК⊥АС
DE=DK
Доказать: Δ АВС - равнобедренный.
Доказательство.
1) DE⊥AB (по условию)  ⇒∠ВЕD = 90° ⇒ ΔВЕD  - прямоугольный,
где BD - гипотенуза, ВЕ,ЕD - катеты.
2) DK⊥AC ( по условию)   ⇒ ∠DKC = 90°  ⇒ ΔDKC - прямоугольный,
где DC - гипотенуза,  СК,КD - катеты.
3) Рассмотрим ΔВЕD и ΔВКС :
DE =DK   (по условию)
ВD = DC = ¹/₂* BC  ( по условию, т.к. т.D - середина ВС)
Следовательно, ΔВЕD = ΔВКС  по 4 признаку равенства прямоугольных треугольников (по  гипотенузе и катету).
Из равенства треугольников  следует , что  ∠В = ∠С .
4)  Рассмотрим Δ АВС : 
∠В  = ∠С  (пункт 3)  - углы при основании АС  
Следовательно,   ΔАВС - равнобедренный, что и требовалось доказать.

№58.
ДАНО :ΔАВС
∠С=90°
ВD - биссектриса
∠F = 90° (по чертежу)
Доказать: DF = DC
Доказательство:
1) Рассмотрим ΔАВС : 
∠С = 90° (по условию) ⇒ΔАСВ - прямоугольный,
где АВ-гипотенуза, АС,СВ - катеты.
ВD  -  биссектриса ∠В   ⇒ делит угол на две равные части:
∠1=∠2 = ¹/₂ *∠В
2)   ΔВFD  - прямоугольный:
∠F=90 , BD - гипотенуза, DF,FB  - катеты.
3)  ΔDCВ - прямоугольный :
 ∠С=90, BD  - гипотенуза ,  ВС,СD  - катеты.
4) ΔBDF = ΔDCB   по 3 признаку равенства прямоугольных треугольников (гипотенузе и острому углу) :
BD  -  общая  сторона
∠1=∠2 = ¹/₂∠В  (пункт 1)
Если треугольники равны, то и соответственные стороны равны:
СВ=DF
DF = DC,  что и требовалось доказать.